In the previous section, you investigated the relationship among the measures of the three interior angles of a triangle.

In this section, you will investigate the relationship between the lengths of the three sides of a triangle and the measures of the three interior angles.

Use the interactive geometry sketch below to investigate the relationship between the length of one side of a triangle and the measure of its opposite angle. Click and drag on any red point to move that vertex and adjust the size and shape of the triangle. Use the sketch to complete the table below. Begin with the side lengths given in the first row of the table, and then use the interactive to create three additional triangles. Use your completed table to answer the questions that follow.

Relationships Between Angle Measures and Side Lengths

In the sketch below, click and drag the red points to adjust the size and shape of the triangle.

Use the sketch to create a triangle. Use the measurements in the sketch to complete the table comparing side lengths and angle measures.

OnTRACK for College Readiness, Created with GeoGebra

Copy and paste the table below into a word processing or spreadsheet app or program. Use the sketch to complete the table. Begin with the side lengths provided. Then, use the sketch to generate three additional triangles.

Interactive popup. Assistance may be required.

See Sample Answers

m∠A	m∠B	m∠C	Angles Measures from Least to Greatest	a	b	c	Side Lengths from Least to Greatest
55.4°	87.3°	37.3°	∠C, ∠A, ∠B	7.8	9.4	5.7	c, a, b
61.7°	52.2°	66.1	∠B, ∠A, ∠C	7	6.3	7.3	b, a, c
37.1°	102.2°	40.7	∠A, ∠C, ∠B	7	11.3	7.6	a, c, b
41.5°	63.7°	74.8	∠A, ∠B, ∠C	4.4	5.9	6.3	a, b, c

Use your completed table to answer the questions that follow.

• In general, what do you notice about the relationship between the angle measures when listed in order from least to greatest and the side lengths when listed in order from least to greatest?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The opposite sides are listed in the same order as the angles.

• In any triangle, which angle is opposite the shortest side?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The smallest interior angle is always opposite the shortest side.

• In any triangle, which angle is opposite the longest side?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The largest interior angle is always opposite the longest side.

Pause and Reflect

In general, what is the relationship between the relative sizes of the interior angles of a triangle and the relative sizes of the sides of a triangle?

Interactive popup. Assistance may be required.

Check Your Answer

The measures of the interior angles of a triangle can be listed in the same order (least to greatest or greatest to least) as the opposite sides of the triangle. In other words, the largest angle is always opposite the longest side, and the smallest angle is always opposite the shortest side.

If you know the interior angle measures of a triangle, can you predict with certainty the lengths of each opposite side? Why or why not?

Interactive popup. Assistance may be required.

Check Your Answer

No. You can only predict the relative sizes of the side lengths, but you cannot directly calculate the side lengths when you only know the three interior angle measures.

If you know the interior angle measures of a triangle, what can you determine about the side lengths of the triangle?

Interactive popup. Assistance may be required.

Check Your Answer

You can determine the shortest side and the longest side of the triangle if you know only the interior angle measures of a triangle.

If you know the side lengths of a triangle, what can you determine about the interior angle measures of the triangle?

Interactive popup. Assistance may be required.

Check Your Answer

You can determine the smallest interior angle and largest interior angle of the triangle if you know only the side lengths of the triangle.

Practice

1. In triangle JKL below, list the side lengths in order from least to greatest.
   
   Interactive popup. Assistance may be required.

   Need a hint?

   Which interior angle is the smallest? Largest?
   Interactive popup. Assistance may be required.

   Check Your Answer

   JK, KL, JL
2. Three towns in Texas, Hillsboro, Corsicana, and Mexia, are connected with highways that create three sides of a triangle. The angle measures between each highway are shown in the figure below.
   

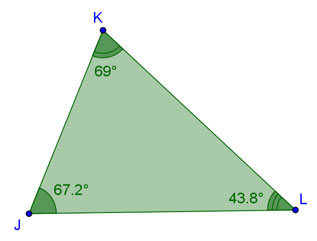
   Based on the information in the figure, which two towns are farthest apart?

   Interactive popup. Assistance may be required.

   Need a hint?

   Which angle is opposite the longest side of a triangle?
   Interactive popup. Assistance may be required.

   Check Your Answer

   Hillsboro and Mexia
3. Three exhibits at a local zoo are connected with sidewalks. The sidewalks create an acute triangle, as shown in the figure below.
   

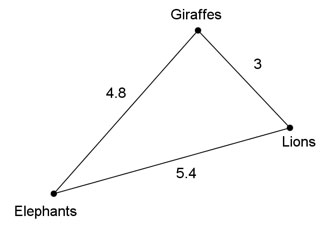
   Which two sidewalks create an angle that is closest to a right angle?

   Interactive popup. Assistance may be required.

   Need a hint?

   How can you determine which interior angle is the largest in a triangle?
   Interactive popup. Assistance may be required.

   Check Your Answer

   The sidewalks at the Giraffes exhibit make an angle that is closest to a right angle.