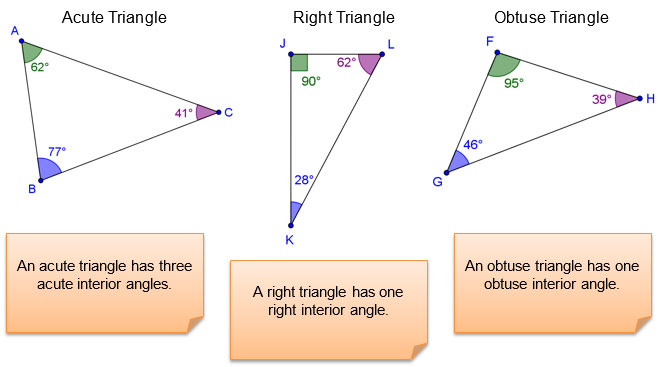
In previous grades, you used angle measures to classify triangles as acute triangles, right triangles, and obtuse triangles.

In this section, you will extend what you know about angle measures and triangles to look for patterns describing the relationship among the measures of the three interior angles in any triangle.

The image below links you to an interactive that you can use to investigate the relationship between the measures of the interior angles of any triangle. Use the interactive to look for a relationship for several different triangles, including at least one acute triangle, at least one right triangle, and at least one obtuse triangle.

• Click and drag on a vertex to change the shape of the triangle.
• Use the slider to rotate two interior angles so that they align with the third interior angle.
• Use the check box to reveal a straight line containing the vertex of the third interior angle.

Interactive popup. Assistance may be required.

Need additional directions?

Use the interactive to answer the following questions.

• When the three interior angles are rotated together so that their vertices line up and they do not overlap, what do you notice about the relationship among the three angles?

  Interactive popup. Assistance may be required.

  Check Your Answer

  When the vertices of the three angles are lined up and they do not overlap, the three angles form a straight line.

• What does this relationship suggest about the sum of the measures of the interior angles for any triangle?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The sum of the measures of the interior angles is 180°.

Pause and Reflect

Write an equation that you can use to relate the measures of interior angles A, B, and C in triangle ABC.

Interactive popup. Assistance may be required.

Check Your Answer

m∠A + m∠B +m∠C = 180°

If you know the measures of two interior angles in a triangle, how could you determine the measure of the third interior angle?

Interactive popup. Assistance may be required.

Check Your Answer

Add the measures of the two known interior angles together and then subtract the sum from 180°.

Practice

1. In the figure below, write an equation that relates the measures of the interior angles and then use your equation to determine the measure of ∠K.
   
   Interactive popup. Assistance may be required.

   Need a hint?

   The sum of the measures of the interior angles of a triangle is 180°.
   Interactive popup. Assistance may be required.

   Check Your Answer

   x + 155.4 = 180
   x = 24.6°
2. A landscape designer is building a triangular shaped flowerbed out of landscaping timbers. The flowerbed is shown in the diagram below.
   

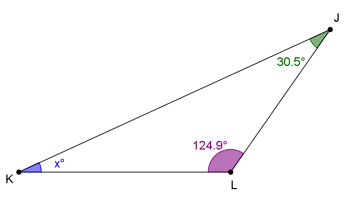
   Two of the interior angles have measures of 38° and 123.8°. What is the measure of the third interior angle?

   Interactive popup. Assistance may be required.

   Need a hint?

   What is the sum of the measures of the three interior angles in a triangle?
   Interactive popup. Assistance may be required.

   Check Your Answer

   x + 161.8 = 180
   x = 18.2°
3. In El Paso, Texas, a shopping center is bordered by three intersecting streets as shown in the diagram below.
   

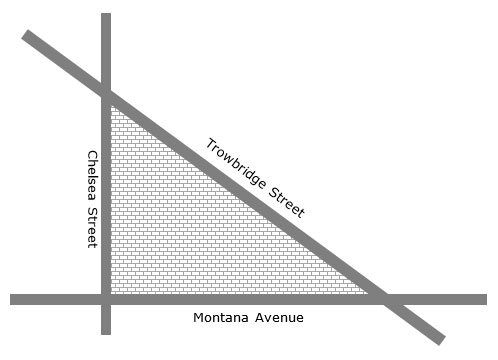
   Chelsea Street and Montana Avenue are perpendicular, and Trowbridge Street and Montana Avenue intersect at an angle of 423 over 4 3 4 °. What is the angle of intersection of Chelsea Street and Trowbridge Street on the corner containing the shopping center?

   Interactive popup. Assistance may be required.

   Need a hint?

   What is the sum of the measures of the interior angles of any triangle?
   Interactive popup. Assistance may be required.

   Check Your Answer

   x + 1323 over 4 3 4 = 180
   x = 471 over 4 1 4 °