In the last section, you applied the area formulas for parallelograms, including rectangles and squares, in order to write equations describing how the area formulas could be used to solve the problems. You also used those equations to determine the solutions to the problems, in some cases using a problem solving process.

In this section, you will apply the area formulas for triangles and trapezoids in order to solve application problems.

Use the interactive below to match each problem situation with an equation. To make the match, drag the correct equation from the column on the right and drop it next to the appropriate problem. Use the reference materials to help you identify the area formulas if necessary.

Use your completed table and the interactive to answer the questions that follow.

• For a triangle, how can you identify the base, b, and height, h, from the figure?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The base is one edge of the triangle, and the height is perpendicular to the base. The height is also the shortest distance between the line containing the base and the vertex of the triangle that is opposite the base.

• For a trapezoid, how can you identify the two bases, b₁ and b₂, and the height, h, from the figure?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The two bases are the parallel edges of the trapezoid. It does not matter which base is b₁ or b₂. The height is the distance between the two bases and is perpendicular to both bases.

Now that you have correctly identified the equations necessary to solve each problem, use the equations to determine the solution to each of the four problems in the interactive.

Click on the problem below to check your solution.

With some word problems involving area, you can use a problem solving model to help you create and implement a plan to solve the problem.

Pause and Reflect

Why do the area formulas for trapezoids and triangles include the factor 1 over 2 1 2 but the area formulas for rectangles and parallelograms do not?

Interactive popup. Assistance may be required.

Check Your Answer

A triangle is one-half of a rectangle.

A trapezoid uses the average length of the bases to calculate the area, and the average of two numbers is one-half the sum of the numbers.

Suppose a triangle has a base length of 16.5 yards and an area of 741 over 4 1 4 square yards. How could you determine the height of the triangle?

Interactive popup. Assistance may be required.

Check Your Answer

Write an equation using the area formula for a triangle, A = 1 over 2 1 2 bh. You know the area, A = 741 over 4 1 4 square yards and the base length, b = 16.5 yards. Substitute these values into the area formula to generate the equation,
741 over 4 1 4 = 1 over 2 1 2 (16.5)h and solve for h.

Practice

1. The Palais du Louvre in Paris, France, has features along the roof above the main entry doors with lateral faces shaped like trapezoids.

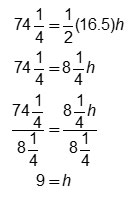
   What is the area of the front face of the roof feature?

   Interactive popup. Assistance may be required.

   Need a hint?

   Use your reference materials to determine the area formula for a trapezoid. Remember that the bases of a trapezoid must be parallel and the height of the trapezoid is the distance between the bases.
   Interactive popup. Assistance may be required.

   Check Your Answer

   A = 1 over 2 1 2 (b₁ + b₂)h
   A = 1 over 2 1 2 (12 m + 21 m)(15.3 m) = 252.45 m²
   The area of the front face of the roof feature is 252.45 square meters.


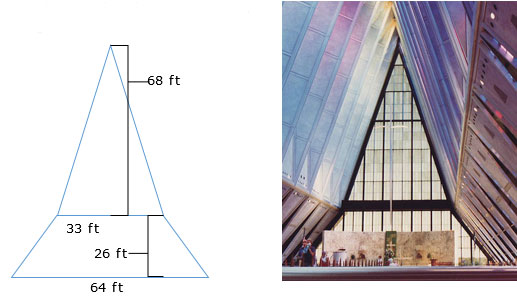
Source: AFChapel, James G. Howes, Wikimedia Commons

2. The Protestant Chapel at the United States Air Force Academy in Colorado Springs, Colorado, contains a large glass window, framed in aluminum, as shown in the diagram below.

   Write two equations that you could use to determine the area of both the triangular and trapezoidal portions of the glass window.

   Interactive popup. Assistance may be required.

   Need a hint?

   Break the window diagram into shapes for which you know area formulas.Then, use the area formulas for a triangle and a trapezoid.
   Interactive popup. Assistance may be required.

   Check Your Answer

   
3. What is the difference between the area of the triangle and the area of the trapezoid? Record your answer in the grid below. Be sure to use the correct place value.
   Interactive popup. Assistance may be required.

   Need a hint?

   Use your equations from Question 2. Calculate the areas of the triangle and the trapezoid, and then subtract the two to find the difference in the areas.