In this section, you will apply the area formulas for parallelograms, including rectangles and squares, in order to solve application problems. To begin, you need to know how to write an expression or equation from an area formula. If you are calculating the area, then you will have an expression that can be simplified using the order of operations. If you know the area and are looking for one of the dimensions, then you can use inverse operations to solve the equation for the unknown dimension.

Use the interactive below to match each problem situation with an equation. To make the match, drag the correct equation from the column on the right and drop it next to the appropriate problem. Use the reference materials to help you identify the area formulas, if necessary.

Use your completed table and the interactive to answer the questions that follow.

• For a parallelogram, how can you identify the base, b, and height, h, from the figure?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The base is one edge of the parallelogram, and the height is perpendicular to the base. The height is not the edge adjacent to the base.

• How can you divide a figure, such as a hexagon that contains all right angles, into rectangles?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Partition the figure into rectangles by extending an edge of the figure from a vertex into the interior of the figure.

• If the reference materials do not contain the area formula for a square, which formula could you use instead? Explain your choice.

  Interactive popup. Assistance may be required.

  Check Your Answer

  Use the area formula for a rectangle, since a square is a special type of rectangle that happens to have all 4 sides congruent.

Now that you have correctly identified the equations necessary to solve each problem, use the equations to determine the solution to each of the four problems in the interactive.

Click on each problem below to check your solution.

With some word problems involving area, you can use a problem solving model to help you create and implement a plan to solve the problem.

A problem solving process has four steps.

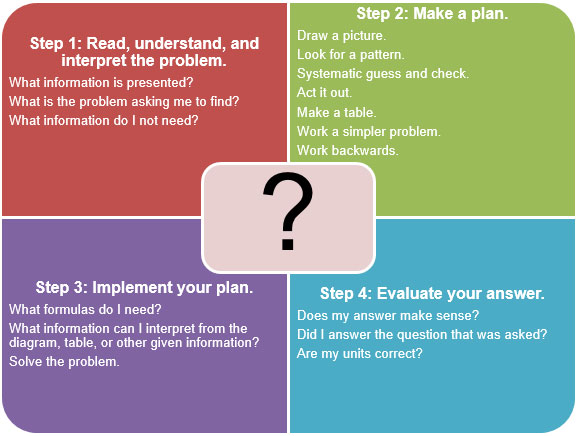
You can use the problem solving process to solve area problems.

Source: Gachado Well Line Camp Adobe House, National Park Service

Pause and Reflect

Why are the area formulas for parallelograms and rectangles the same?

Interactive popup. Assistance may be required.

Check Your Answer

If you slice a triangle off a parallelogram and move it to the other end of the parallelogram, then it makes a rectangle with the same dimensions as the parallelogram.

Suppose a parallelogram has a base length of 16.5 yards and an area of 741 over 4 1 4 square yards. How could you determine the height of the parallelogram?

Interactive popup. Assistance may be required.

Check Your Answer

Write an equation using the area formula for a parallelogram, A = bh. You know the area, A, = 741 over 4 1 4 square yards and the base length, b, = 16.5 yards. Substitute these values into the area formula to generate the equation,
741 over 4 1 4 = 16.5h and solve for h.

Practice

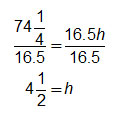
Source: John Hancock Tower, Tomtheman5, Wikimedia Commons

1. The roof and ground floor of the John Hancock Tower in Boston, Massachusetts, are in the shape of a parallelogram. If the roof is represented by the diagram below, what is the area of the roof of the John Hancock Tower?
   Interactive popup. Assistance may be required.

   Need a hint?

   Use your reference materials to determine the area formula for a parallelogram. Remember that the base and height of a parallelogram must be perpendicular.
   Interactive popup. Assistance may be required.

   Check Your Answer

   A = bh
   A = (310 feet)(100 feet) = 31,000 square feet
   The area of the roof of the John Hancock Tower in Boston is 31,000 square feet.
2. The first floor of Independence Hall in Philadelphia, Pennsylvania, is shown in the diagram below.
   

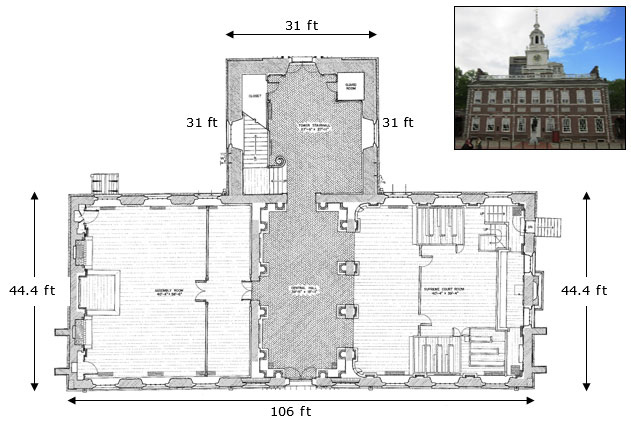
   Source: HABS measured drawing of the first floor of Independence Hall, Library of Congress, Wikimedia Commons

   Write an equation that you could use to determine the area of the first floor of Independence Hall.

   Interactive popup. Assistance may be required.

   Need a hint?

   Break the first floor diagram into rectangles, and then use the area formula for a rectangle.
   Interactive popup. Assistance may be required.

   Check Your Answer

   
   Total Area = Area of Square + Area of Rectangle
   A = (31)(31) + (106)(44.4)
3. What is the area of the first floor of Independence Hall in square feet? Record your answer in the grid below. Be sure to use the correct place value.
   Interactive popup. Assistance may be required.

   Need a hint?

   Use your equation from Question 2. Follow the order of operations to simplify the right-hand side of the equation.