
In this section, you will compare the perimeter and area of similar figures.
If you were looking at the perimeters between a figure and its enlargement or reduction, then the scale factor, which describes the change in the dimensions, is the same for the perimeter.
Since the perimeter is the same as the sum of the linear measurements of length and width, all the dimensions were changed proportionately.

Perimeter = 8 + 10 + 8 + 10 = 36
Perimeter = 4 + 5 + 4 + 5 = 18
Area, on the other hand, is a 2-dimensional measurement. In the rectangles shown in the illustration below, both the length and width are reduced by a factor of 1 2 .
The area is then reduced by a factor of 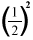 or
1
4
.
or
1
4
.
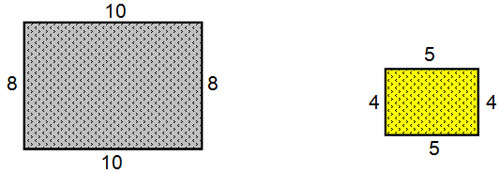
Area = (8)(10) = 80
Area = (4)(5) = 20
80 × 1 4 = 20
In the case of circles, or figures which do not have a definite pair of dimensions like width and length, you still square the scale factor when considering area.
The figures shown below represent 2 sizes of pizzas sold at a restaurant. The diameters of the pizzas are 8 inches and 12 inches. How much larger is the 12-inch pizza than the 8-inch pizza? Hint: Compare the areas.
