
In this section, you will review similar figures and compare their area as well as discuss the vocabulary used to describe similar figures.
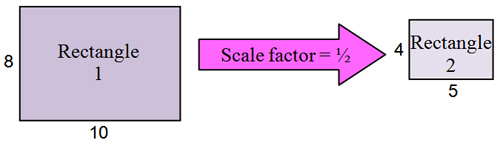
Similar figures are the same shape but not necessarily the same size. Consider the two rectangles shown below.

The angles in rectangle 1 are congruent to the angles in rectangle 2, but the sides are not congruent. However, we say that the sides are proportional because the ratios of the corresponding sides are equivalent as shown below. Therefore, the rectangles are similar. 8 4 = 10 5
Once you know that two figures are similar, you can determine a scale factor which will describe the amount by which one figure has been enlarged or reduced to achieve the second figure.
In the example above, Rectangle 1 has been reduced by a scale factor of 1 2 to get Rectangle 2. The dimensions (length and width) of Rectangle 2 are each 1 2 the dimensions of Rectangle 1.
Lengths: 10 x 1 2 = 5
Widths: 8 x 1 2 = 4
This holds true of the perimeter as well. Rectangle 1, the perimeter is 2(8) + 2(10) = 36. Rectangle 2, the perimeter is 2(4) + 2(5) = 18.
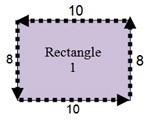
Perimeter Rectangle 1 = 8 + 10 + 8 + 10 = 36
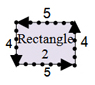
Perimeter Rectangle 2 = 4 + 5 + 4 + 5 = 18
Whether a change is a reduction or an enlargement, the perimeter will change by the same scale factor.
Caution! The change in the perimeter matches the change in the dimensions from one figure to the next ONLY if both dimensions are changed in the same way.
