In the last section, you investigated dilations, or methods of generating similar figures using scale factors. In this section, you will look into specific patterns that occur for dilations of figures on a coordinate plane.

Click on the geometry sketch below to investigate what happens when the red triangle, ABC, is dilated by different scale factors.

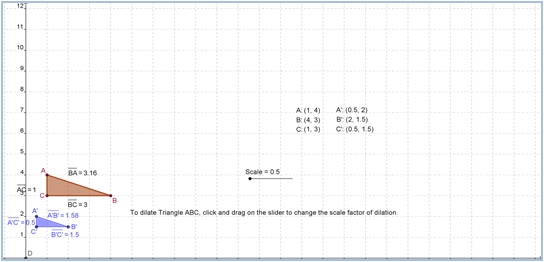
• Use the slider in the sketch to change the scale factor from the red triangle ABC to the dilated blue triangle A’B’C’.
• As you do, record the lengths of the sides and the coordinates of the points in a table like the one shown below. You may create the table in your notes.
• As you complete the table, notice that when triangle A’B’C’ is dilated by a scale factor of 1, it is congruent to the original triangle ABC. You will use that to look for patterns in the table

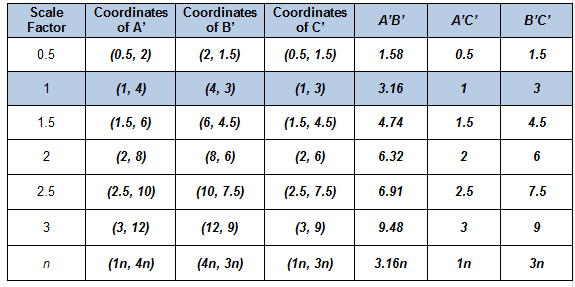
Click on the chart to check your answers.

1. For each scale factor, how do the coordinates of the dilated vertices A’, B’, and C’ relate to the coordinates of the original vertices A, B, and C?
Interactive popup. Assistance may be required.
Check Your Answer
The coordinates of the dilated vertices are equal to the coordinates of the original vertices, A, B, and C, multiplied by that scale factor.
2. For a scale factor of n, what would the coordinates of the vertices A’, B’, and C’ be in terms of n and the original coordinates?
Interactive popup. Assistance may be required.
Check Your Answer
For a scale factor n, the coordinates of triangle A’B’C’ would be:
A’ (1n, 4n) = n × coordinates of A
B’ (4n, 3n) = n × coordinates of B
C’ (1n, 3n) = n × coordinates of C
3. For each scale factor, how do the side lengths of the dilated triangle A’B’C’ relate to the side lengths of the original triangle ABC?
Interactive popup. Assistance may be required.
Check Your Answer
The side lengths of the dilated triangle A’B’C’ are equal to the side lengths of the original triangle ABC, multiplied by that scale factor.
4. For a scale factor of n, what would the side lengths of the dilated triangle A’B’C’ be in terms of n and the original side lengths?
Interactive popup. Assistance may be required.
Check Your Answer
For a scale factor n, the side lengths of triangle A’B’C’ would be:
A’B’ = 3.16n = n × AB
A’C’ = 1n = n × AC
B’C’ = 3n = n × BC
5. Use your answers to Questions 2 and 4 to complete the row for a scale factor of n in your table if you have not already done so.

Journal Entry

Generalize the relationships for coordinate dilations for any figure, not just triangle ABC. What happens to the coordinates of a figure when it is dilated by a scale factor of n? What happens to the side lengths?

Interactive popup. Assistance may be required.

Check Your Answer

The coordinates of the vertices of the dilated figure are equal to the coordinates of the original vertices multiplied by the scale factor n. The side lengths of the dilated figure are equal to the side lengths of the original figure multiplied by the scale factor n.