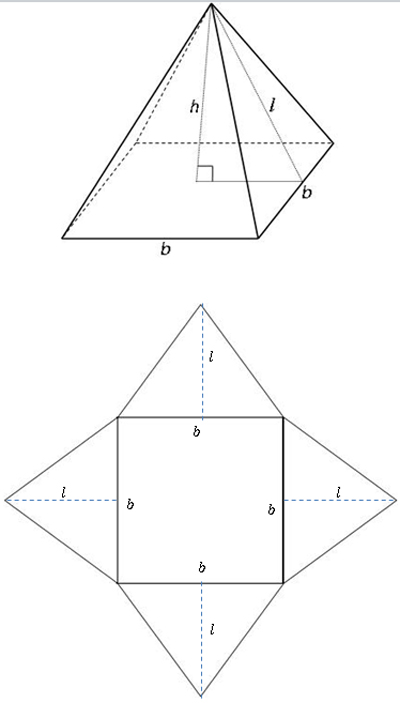
Below is a picture of a pyramid and the net of a pyramid. The difference between a prism and a pyramid is a pyramid has only one base and the lateral faces are always triangles. The diagram below shows a square pyramid, or a pyramid whose base is a square. Notice the variables used to label the sides. The letter b is used to label the side of the square, h is used to label the height of the pyramid, and l is used to label the slant height.

Want to know more about pyramids?
Answer the following questions. Click on the blank space to check your answers.




The area of each of the triangular faces is A = 1 2 b • h, where b and h are the base and height of the triangle. Since there is also a height of the pyramid itself, let h represent the height. We will need to use l to represent the height of the triangle since the height of the triangle (which is a lateral face of the pyramid) is also the slant height of the pyramid.
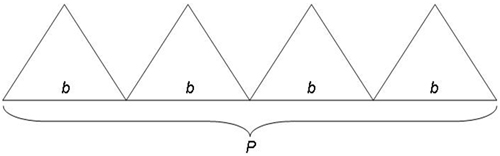
There is a formula to find the total surface area of a pyramid. First, find the area of all the triangles at one time. The sum of the lengths of the bases of the triangle always form the perimeter, P, of the pyramid. To find the area of all of the triangles in one step the formula for the area of a triangle, A = 1 2 b • h, where b and h, is used with P replacing b and l replacing h or A = 1 2 P • l.
The next step is to find the area of the square base, B. The area of a square is B = s2 = b • b
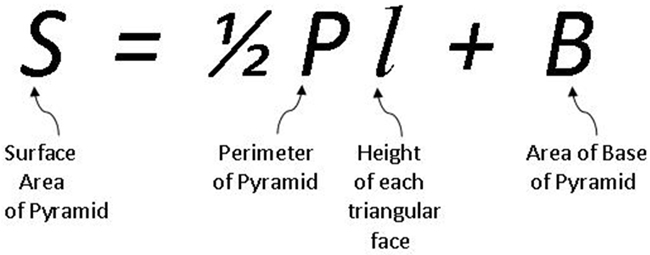
The formula incorporating both steps is: S = 1 2 Pl + B
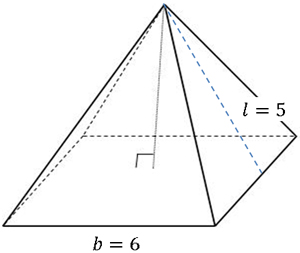
Example: Given a square pyramid with b = 6 and l = 5, find the total surface area.
Answer the following questions. Click on the blank space to check your answers.





