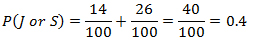
Now that we’ve looked at simple probability, let’s look at what happens when there is more than one thing happening at a time.
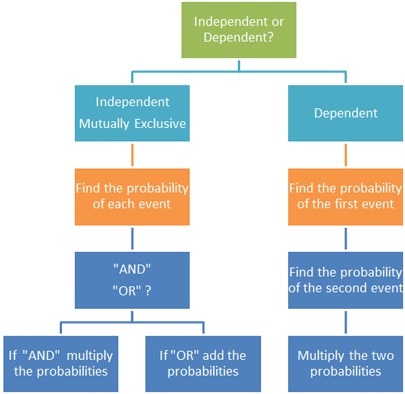
When there are two events happening, the first thing is to determine if one depends on the other or if they are independent.
If they are independent of each other, they are called mutually exclusive. If one event depends on the other event, then we have conditional probability.
The flowchart below will help you determine what to do in each situation. Copy this into your e-journal for reference.

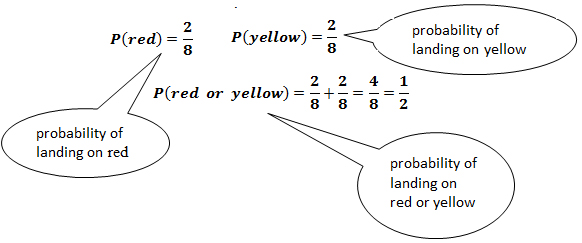
A spinner spins twice—each spin has an equal chance of landing on a particular color.
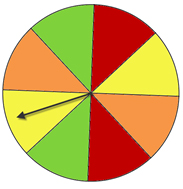
What is the probability of the above spinner landing on yellow both times in two spins? (This is an "AND" situation, so we'll multiply the probabilities together.

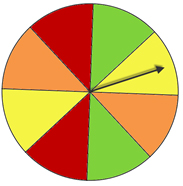
A spinner spins twice—each spin has an equal chance of landing on a particular color.
What is the probability of the spinner landing on either red or yellow? (This is an "OR" situation, so we'll add the probabilities together.)

A card is drawn from a deck of cards, not replaced, and a second card is drawn from the deck. The probability of the second event is different from the first event because there is one fewer card in the deck.
What is the probability of first drawing a Queen from the deck, not replacing it, and then drawing a 5?
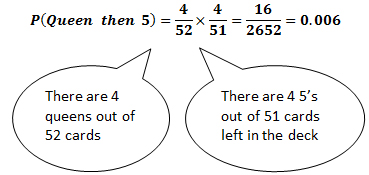
Try it...

Source: Marbles, Joe Mabel, Wikimedia
A jar has 6 red marbles and 4 green marbles. Two marbles are drawn without replacement from the jar. What is the probability that both of the marbles are green?
Interactive popup. Assistance may be required.
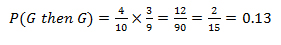

A jar has 6 red marbles and 4 green marbles. This time once marbles are drawn they are replaced back in the jar. What is the probability that both the marbles are green?
Interactive popup. Assistance may be required.
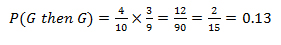


Tom and Christine have a backyard chicken coop. They've collected a basket that has 13 brown eggs and 23 white eggs. Assuming he selects randomly, what is the probability that Tom picks a white egg, then a brown egg for breakfast?
Interactive popup. Assistance may be required.
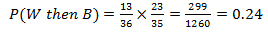

If Tom does get a white egg then a brown egg, what is the probability that Christine will also get first a white egg, then a brown one?
Interactive popup. Assistance may be required.
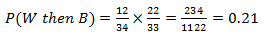

A high school counselor working with student records noticed that 14% of the student body was made up of seniors, 26% made up of juniors, 36% made up of sophomores and the rest were freshmen. If she randomly selects two student names from the records to act as greeters to greet new students enrolling in the school, what are the chances that the names she selects will be either a junior or senior?
Interactive popup. Assistance may be required.