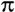 d = 2
d = 2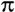 r
.
r
.
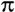 = 16
= 16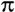 = 50.3 cm
.
= 50.3 cm
.
In this section, a proportion is used to find the arc length. A calculator is needed.
A proportion written in the form Part 1 Whole 1 = Part 2 Whole 2 can be used to find the length of an arc. Part 1 and Whole 1 are usually what we know. Part 2 and Whole 2 include one unknown piece of information.
Proportion and Cross Product Review
Example: Use the information obtained in section one to find the arc length of the blue M&Ms on the circle.
Below is a chart with the information obtained in section 1.
| Color | Number | Fraction of Total |
| Red | 6 | 6 25 |
| Blue | 5 | 5 25 = 1 5 |
| Green | 6 | 6 25 |
| Yellow | 4 | 4 25 |
| Brown | 4 | 4 25 |
| Total | 25 | 25 25 = 1 |
Part 1 is the number of a certain color (blue) of M&Ms and Whole 1 is the total number of M&Ms.
Part 1 Whole 1 = Number of a certain color of M&M All the M&Ms
The variable, or information that we don't know, is part of the second fraction: Part 2 Whole 2
Three out of the four pieces of information must be known in order to solve a proportion.
Fill in the following. Use the variable x or y for unknown values. Click on the blanks to reveal the answers.
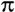 d = 2
d = 2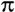 r
.
r
.
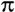 = 16
= 16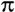 = 50.3 cm
.
= 50.3 cm
.
A general equation to find the length of an arc is:
Degree measure of the sector360° in a circle = Measure of arc length Circumference of circle
Example: Given the circle below, find the arc length of the shaded part of arc AB.
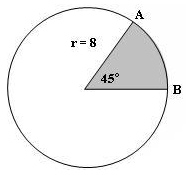
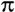 r = 2
r = 2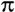 (8) = 16
(8) = 16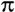 = 50.2cm
= 50.2cm
Check logically: