A sector is a portion of a circle. There is a relationship between the central angle that creates the sector, the area of the sector, and the area of the circle. In this section of the lesson, you will investigate that relationship.

Use the dynamic geometry sketch below in order to complete the table that follows. To do so, use a circle with a radius of 3 units. To fill in the table, you may copy it into your notes. Use the information in the table to answer the conclusion questions that follow.

Area of Sector Investigation

Click and drag the Radius slider to change the radius of the circle. Click and drag the Angle slider to change the measure of the central angle.

Interactive popup. Assistance may be required.

Need additional directions?

Interactive popup. Assistance may be required.

Check Your Answer

Conclusion Questions

• How do the two ratios, Measure of Central Angle over 360 Measure of Central Angle 360 and Area of Sector over Area of Circle Area of Sector Area of Circle , compare?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The two ratios are approximately equal.

• Is the relationship between the measure of the central angle, the area of the sector, and the area of the circle proportional? How can you tell?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Yes, the relationship is proportional because the two ratios are equal.

• Write an equation that describes the relationship between the measure of the central angle, the area of the sector, and the area of the circle.

  Interactive popup. Assistance may be required.

  Check Your Answer

  Measure of Central Angle over 360 Measure of Central Angle 360 = Area of Sector over Area of Circle Area of Sector Area of Circle

Pause and Reflect

Does the relationship between the measure of the central angle, the area of the sector, and the area of the circle change if the radius of the circle changes? Why or why not?

Interactive popup. Assistance may be required.

Check Your Answer

No, because the proportional relationship will be true regardless of the size of the circle.

Rewrite your proportion in the form of an equation that you can use to calculate the area of the sector.

Interactive popup. Assistance may be required.

Check Your Answer

Area of Sector = Measure of Central Angle over 360 Measure of Central Angle 360 × Area of Circle

Practice

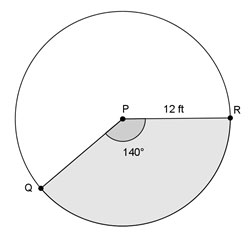
Use the relationship from this section to answer the following questions.

1. Determine the area of sector QPR in circle P shown below.
   
   
   
   Interactive popup. Assistance may be required.

   Need a hint?

   Use the equation, Area of Sector = Measure of Central Angle over 360 Measure of Central Angle 360 × Area of Circle.
   Interactive popup. Assistance may be required.

   Check Your Answer

   
2. A circular fountain is divided into two portions as shown in the diagram.
   
   
   

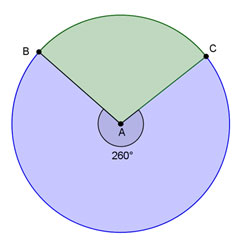
   If the fountain has a diameter of 9 yards, what is the area of the sector BAC shown in green?

   Interactive popup. Assistance may be required.

   Need a hint?

   A full circle has 360° of rotation at its center, and you need to use the radius to calculate the area of a circle.
   Interactive popup. Assistance may be required.

   Check Your Answer

   
3. The circumference of a circular walking path around a city park is 112 meters. Inside the walking path, there is a rock sculpture garden in the shape of a sector of the circle with a 40° central angle. To the nearest square meter, what is the approximate area of the rock sculpture garden?

   Interactive popup. Assistance may be required.

   Need a hint?

   Draw a picture to help you. The formula for the circumference of a circle is C = 2π r, and you can use the radius from this formula to calculate the area of the circle.
   Interactive popup. Assistance may be required.

   Check Your Answer