In this resource you are going to look at how to find the area of composite figures. This means that sometime you will have to add the area of figures together and sometimes you will need to subtract the area of a figure from the area of a larger figure. Before we start, let's review what you already know about area. Your Mathematics Chart and other formula reference charts contain formulas for certain common polygons. Match the polygon with its figure and area formula. To do so, click and drag the polygon and the area formula onto the appropriate spot on the table.

Let's look at the rectangle and triangle below:

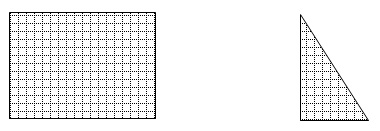
We learned that in order to find the area of the rectangle, you must multiply the length of the base by the length of the height. We also learned that to find the area of the triangle we had to multiply the length of the base by the length of the height and then divide the product by 2.

Think about what would happen if we combined the shape of the rectangle with the shape of the triangle. Our shape could look something like the composite figure below.

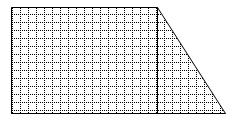
Think about how you would find the area of the figure.

Pause and Reflect

You can find the area of a figure like the one shown in two ways: either as a rectangle and a triangle separately, then add the areas together, or think of the figure as a trapezoid. How do these two methods compare? Which one do you think is easier to use?

Possible Response When the triangle and rectangle are adjacent as shown in the figure, the bottom base is longer than the top base. The bottom base is equal to the base of the rectangle added to the base of the triangle. For a trapezoid, we would call this new base "base 2" and use its length for b₂ in the area formula.


Which method is easier? That depends on the information you are given and your experience with solving area problems! Either way is correct!
Close

Let's look at another composite figure using the rectangle and the triangle above. Sometimes people call these "shady things" since the composite figure has a shaded figure in its interior.

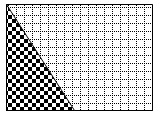
Pause and Reflect

How could you find the area of the rectangle without the triangle?

Possible Response Find the area of the rectangle and the area of the triangle, then subtract the area of the triangle from the area of the rectangle.
Close