In previous math courses, you learned about the formulas for area and circumference of circles. In this lesson, you will revisit those formulas and compare them to the area formula for regular polygons.

Use this applet, which will allow you to manipulate the radius of the circle by clicking and dragging on the flashing point while it calculates the circumference and area of the circle. Use this applet to refresh your knowledge of finding the area of a circle.

Next, you will revisit the applet from earlier in the lesson that allowed you to investigate the relationship between the side length, perimeter, apothem, and area of regular polygons.

In the applet linked to the image below, check the boxes to show the apothem and the side length. Use the applet below to increase the number of sides of the regular polygon. As you do so, pay attention to the shape of the regular polygon and the relationship between the radius of the polygon and the apothem of the polygon.

Interactive popup. Assistance may be required. Click here for additional directions.

Use the information in the interactive you just completed to answer the following questions.

• As the number of sides of the regular polygon increases, what happens to the shape of the regular polygon?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The shape of the regular polygon appears to round out and look more like a circle.

• As the number of sides of the regular polygon increases, how does the radius compare to the apothem of the polygon?

  Interactive popup. Assistance may be required.

  Check Your Answer

  As the number of sides of the regular polygon increases, the radius and the apothem become very close to the same number.

• The area formula for a regular polygon is A = 1 over 2 1 2 Pa. The perimeter of the regular polygon approaches the circumference of a circle, C = 2πr, and the apothem of the regular polygon approaches the radius of a circle, r, as the number of sides gets larger and larger. Substitute circumference for P and the radius for the apothem of the regular polygon, and simplify the expression. What do you notice?

  Interactive popup. Assistance may be required.

  Check Your Answer

  If you substitute these values into the area formula for the regular polygon, you can simplify the formula as follows.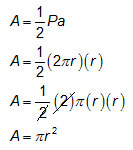
  
  
  
  This expression is the same as the formula for the area of a circle.

Pause and Reflect

As the number of sides of a regular polygon increases and you keep the radius of the polygon the same, why do you think the regular polygon becomes more circular?

Interactive popup. Assistance may be required.

Check Your Answer

If you keep the radius the same, the sides become shorter as the number of sides increases. This makes the polygon look like it is getting round like a circle.

Practice

Determine the area of each figure below.

1. A square has the same center and radius as a circle with a diameter of 10 inches. This square is called an inscribed square inside the circle. What is the area of the circle that is outside the square?

Interactive popup. Assistance may be required.

Need a hint?

Determine the area of the circle and the area of the square, and then subtract the area of the square from the area of the circle.

Interactive popup. Assistance may be required.

Check Your Answer

2. A computer manufacturing company puts small plastic washers on all of the bolts that are used to construct their computer parts. The plastic washer is a circle with an inscribed regular hexagonal shaped hole that is cut out of the center. If the radius of the circle is 16 millimeters, what is the area of the plastic washer?

Interactive popup. Assistance may be required.

Need a hint?

Determine the area of the circle and the area of the hexagon, and then subtract the area of the hexagon from the area of the circle.

Interactive popup. Assistance may be required.

Check Your Answer

Washer Solution