A common regular polygon for which you will need to use trigonometry to find the length of the apothem is an octagon. Watch the following video to see how the trigonometric relationships are used to find the apothem.Unfortunately, not every regular polygon can be divided into equal special right triangles. For the non-special right triangles, you will need to use trigonometric relationships among the side lengths in right triangles in order to determine the length of the apothem.
A common regular polygon for which you will need to use trigonometry to find the length of the apothem is an octagon. Watch the following video to see how the trigonometric relationships are used to find the apothem.
Source: Area of Regular Polygons, calculatorbox, YouTube
Interactive popup. Assistance may be required.
For a hexagon, the central angle of each interior triangle is 60°. When the 60° central angle is bisected by the apothem, you are left with a 30° angle inside a right triangle. For an octagon, the central angle of each interior triangle is 45°. When the 45° central angle is bisected by the apothem, you are left with a 22.5° angle inside a right triangle.
Interactive popup. Assistance may be required.
Tangent
Interactive popup. Assistance may be required.
You should use 1 over 1 2 the side length of the regular polygon because the apothem bisects the side length to create a right triangle.
Determine the area of each regular polygon below.
1.
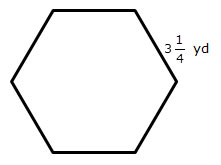
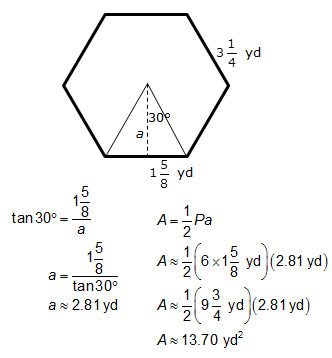
Interactive popup. Assistance may be required.
You are given the side length of a regular hexagon, so you can use either trigonometry or special right triangles to determine the length of the apothem in order to calculate the area of the regular hexagon.
Interactive popup. Assistance may be required.
2. A swimming pool is in the shape of a regular octagon with a side length of 15 feet. What is the area of the surface of the swimming pool?
Interactive popup. Assistance may be required.
Draw a figure. Use trigonometric ratios to determine the length of the apothem of the octagon.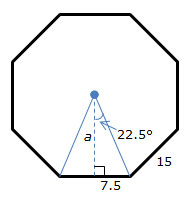
Interactive popup. Assistance may be required.
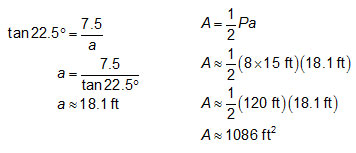
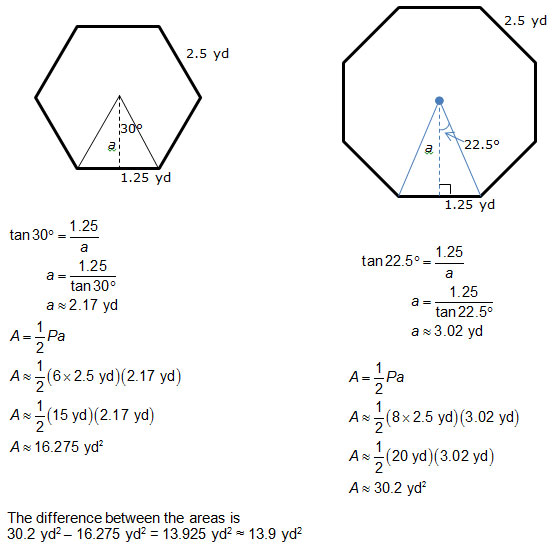
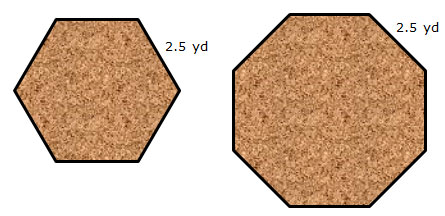
3. Marshawn has designed two rugs that are in the shape of a regular hexagon and a regular octagon, each with a side length of 2.5 yards. How much greater is the area of the octagonal rug than the area of the hexagonal rug? Round your answer to the nearest tenth of a square yard.
Interactive popup. Assistance may be required.
Use the area formula for a regular polygon, A = 1 over 2 1 2 Pa, to determine the area of each rug. You will need to use trigonometry to determine the length of the apothem of the regular octagon, and you can either use trigonometry or special right triangles to determine the length of the apothem of the regular hexagon.
Interactive popup. Assistance may be required.
