Now we will use your knowledge of the area of a triangle and special right triangles to find the area of regular polygons of more than 4 sides. In order to accomplish this task, let's first look at a couple of different measurements that you can take on the interior and exterior of a polygon.
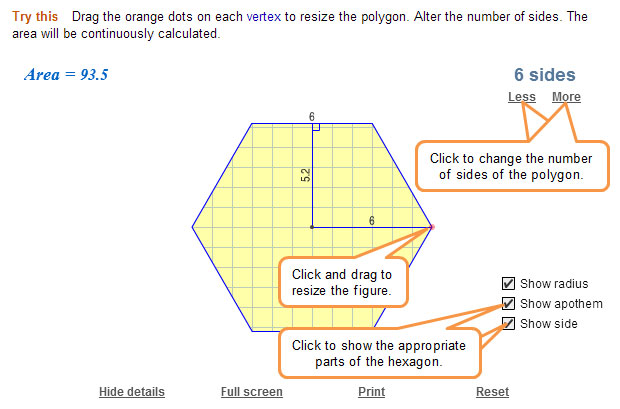
Click on the image to access the applet. Use the applet below to generate the length of the radius, apothem, and side length for a regular polygon. The applet begins with a hexagon and will calculate the area for you. Drag the orange dot that represents a vertex of the hexagon to change the size of the hexagon. Use the information from the applet to complete the table for hexagons beneath the image, and then use that table to answer the two questions which follow.
Interactive popup. Assistance may be required.
Click for additional directions.
Side Length |
Perimeter |
1 over 2
1
2
perimeter |
Apothem |
Area |
6 |
36 |
18 |
5.2 |
93.5 |
7.5 |
||||
4 |
||||
5.8 |
||||
7.8 |
Side Length |
Perimeter |
1 over 2
1
2
perimeter |
Apothem |
Area |
6 |
36 |
18 |
5.2 |
93.5 |
7.5 |
45 |
22.5 |
6.5 |
146.5 |
4 |
24 |
12 |
3.5 |
41.6 |
5.8 |
34.8 |
17.4 |
5 |
87.4 |
7.8 |
46.8 |
23.4 |
6.7 |
158.1 |
Interactive popup. Assistance may be required.
The area is approximately equal to the product of the apothem and 1 over 2 1 2 perimeter.
Interactive popup. Assistance may be required.
A = 1 over 2 1 2 Pa
The animation below will show how the formula that you generalized from the formula you generalized from the table relates to the side length, perimeter, and apothem of a regular hexagon.
Watch the video below to see how the area of a regular hexagon can be determined using a variety of methods.
Source: Areas of Regular Polygons, fractad, YouTube
You used a table with number patterns to inductively develop the area formula for a regular polygon and verified the formula geometrically. If the number of sides changed from 6 to 8, do you think the formula would still be true? Why or why not?
Interactive popup. Assistance may be required.
Yes, the formula would still be true. Any regular polygon, including an octagon, can be divided into its component triangles and rearranged into a parallelogram with a base length of 1 over 2 1 2 the perimeter and a height equal to the apothem of the regular polygon.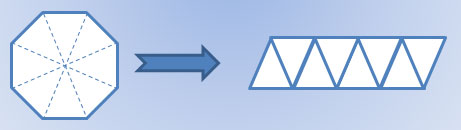
Determine the area of each figure below.
1.
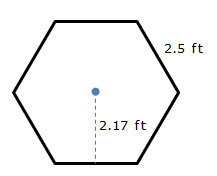
Interactive popup. Assistance may be required.
Use the information given to determine the perimeter and the apothem of the regular hexagon. You are given the length of one side and the length of the apothem.
Interactive popup. Assistance may be required.
A = 1 over 2 1 2 Pa
2. Beasley constructed a regular hexagon with a side length of 16 centimeters. What is the area of the regular hexagon?
Interactive popup. Assistance may be required.
Draw a figure. Use the properties of 30-60-90 triangles to determine the length of the apothem of the hexagon.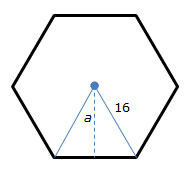
Interactive popup. Assistance may be required.
| a = 1 over 2
1
2
s√3 a = 1 over 2 1 2 (16 cm)√3 a = 8√3 ≅ 13.9 cm |
A = 1 over 2
1
2
Pa A = 1 over 2 1 2 (6 × 16 cm)(8√3 cm) A1 over 2 1 2 (96 cm)(8√3 cm) A = 384√3 cm2 ≅ 665.1 cm2 |
3. The traffic sign below is in the shape of a regular octagon with a side length of 18 inches and an apothem of 21.7 inches. If the sign is composed of flat sheet metal, what is the amount of metal required to manufacture 1 sign for a traffic intersection?
Interactive popup. Assistance may be required.
Use the area formula for a regular polygon, A = 1 over 2 1 2 Pa.
Interactive popup. Assistance may be required.
A = 1 over 1 2 Pa