Look at the triangles below. Where are the base and height for each of these triangles? Click the View animation button beneath each triangle to check your answers.
Let’s begin our study of area with triangles. As you work with regular polygons in this lesson, you will frequently use triangles. We will begin this lesson by considering the area of triangles from a variety of perspectives and representations.
As seen in the introduction to this lesson, the area formula for a triangle is A = 1 over 2 1 2 bh. To find the area of a triangle, you must be able to locate the base and height.
Look at the triangles below. Where are the base and height for each of these triangles? Click the View animation button beneath each triangle to check your answers.
Another item that you will need to know is the relationship among the sides of special right triangles. If you need to review the special right triangles relationships in greater detail, then refer to module 2, lesson 3.
There are two distinct relationships found in special right triangles. The first relationship deals with 45-45-90 triangles which have two 45° angles and a 90° angle. The second relationship deals with 30-60-90 triangles where the three angles measure 30°, 60°, and 90°.
Drag the label for each side of the triangles below to the side of the triangle that it best describes. Click the Reset button for each triangle if you need to reset the interactive.
Interactive popup. Assistance may be required.
The base and height are the legs of the triangle, each of which measures x units.
Interactive popup. Assistance may be required.
The base and height are the two legs of the triangle, which have length x units and x √3units respectively.
How are a 30-60-90 triangle and an equilateral triangle related?
Interactive popup. Assistance may be required.
A 30-60-90 triangle is half of an equilateral triangle. If you folded an equilateral triangle along one of its altitudes, you would generate a 30-60-90 triangle.
How could you use a 30-60-90 triangle to determine the area of an equilateral triangle?
Interactive popup. Assistance may be required.
If you know the side length of an equilateral triangle, you can determine the length of the altitude (height) of the equilateral triangle by dividing the side length by 2 and multiplying by √3.
Determine the area of each figure below.
1.
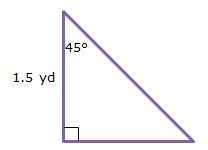
Interactive popup. Assistance may be required.
What are the lengths of the base and height of this triangle? Use what you know about special right triangles to determine those dimensions.
Interactive popup. Assistance may be required.
A = 1 over 2 1 2 bh
2.
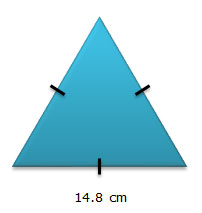
Interactive popup. Assistance may be required.
The congruence marks indicate that this is an equilateral triangle, so use the properties of a 30-60-90 triangle to determine the height of the equilateral triangle.
Interactive popup. Assistance may be required.
| h = 1 over 2
1
2
b√3 h = 1 over 2 1 2 (14.8 cm)√3 h = 7.4√3 ≅ 12.8 cm |
A = 1 over 2
1
2
bh A ≅ 1 over 2 1 2 (14.8 cm)(12.8 cm) A ≅ 94.72 cm2 |
3. The traffic sign below is in the shape of an equilateral triangle with a side length of 24 inches. If the sign is composed of flat sheet metal, what is the amount of metal required to manufacture 4 signs for a traffic intersection?
Interactive popup. Assistance may be required.
Use the properties of a 30-60-90 triangle to determine the height of the equilateral triangle. The amount of sheet metal required to manufacture one sign is the area of one sign. Once you know the area of one sign, you can use that information to determine the area of 4 signs.
Interactive popup. Assistance may be required.
| h = 1 over 2
1
2
b√3 h = 1 over 2 1 2 (24 in.)√3 h = 12√3 in. |
A = 1 over 2
1
2
bh A = 1 over 2 1 2 (12√3in.)(24 in.) A = 144√3 in.2 |
| Total Area for 4 Signs = 4 × 144√3 in.2 = 576√3 in.2 ≅ 997.7 in.2 | |