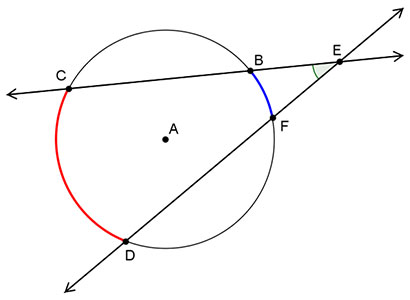
You have generalized the arc and angle relationships found from intersecting lines inside of a circle. Now let’s explore the possible relationships found by intersecting lines outside of a circle. In this section, you will use inductive reasoning to write a formula relating the measure of the angle between two secants that intersect outside a circle to the measures of the intercepted arcs.
In the diagram at right,
EC and
ED are secants to circle A that create intercepted arcs
BF and
CD.
Before you begin, write out a hypothesis for the relationship between the angle formed when two secants intersect outside of the circle and the intercepted arcs that are formed. Look at the figures below.
When secant lines intersect inside of circle, the measure of the interior angle is half the sum of the arc measures.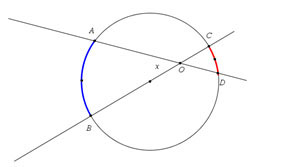 
x = 1 over 2
1
2
(m
AB +
m
CD) |
Use this diagram as an example. In your notes, write out a hypothesis that relates the measure in intercepted arcs and the angle of intersection at  |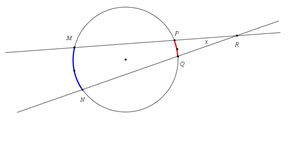
Now let’s explore!
Using the Intersecting Secants applet linked below, manipulate the endpoints of
AB so that you will always have two secants, and the blue and red arcs are opposite of each other on the circle. Observe the changes in m∠D as you change the arc measurements.
On the right side of the applet, notice the generalizations that are stated as you explore.
Click on the image below to open the applet. Manipulate the angle so that m∠D is 30 degrees, then 40 degrees, and finally 50 degrees.
| m ∠ D | m
AB |
m
EC |
m
AB – m
EC |
| 30° | |||
| 40° | |||
| 50° |
AB - m
CE ?
Interactive popup. Assistance may be required.
m∠D = 1 over 2 1 2 (mAB – m
CE)
AB and
CE are the intercepted arcs of the two secants, what can you say about the measure of the angle between two intersecting secants and the measures of the intercepted arcs?
Interactive popup. Assistance may be required.
If two secants intersect outside a circle, then the measure of the angle formed is equal to half the difference of the measures of the intercepted arcs.
How does the relationship that you discovered for two secants that intersect outside a circle compare to the relationships you discovered for two secants (or chords) that intersect inside a circle?
Interactive popup. Assistance may be required.
If the point of intersection is outside the circle, then the angle measure is one-half the difference of the intercepted arc measures. If the point of intersection is inside the circle, then the angle measure is one-half the sum of the intercepted arc measures.
BC and
FD are two secants of circle A that intersect at point E.
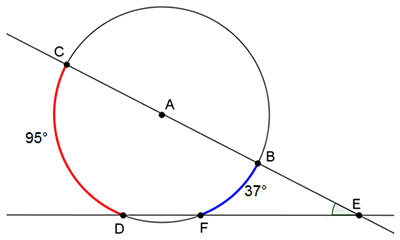
What is m∠BEF?
Interactive popup. Assistance may be required.
The measure of the angle between two secants that intersect outside a circle is one-half the difference of the measures of the intercepted arcs.
Interactive popup. Assistance may be required.
m∠BEF = 1 over 2 1 2 (mCD – m
BF)
ZP and
ZQ are two secants of circle M that intersect at point Z and m∠PZQ = 61.8°.
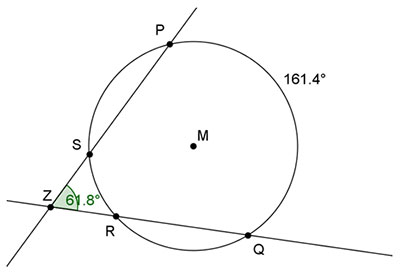
What is m
RS?
Interactive popup. Assistance may be required.
The measure of the angle between two secants that intersect outside a circle is one-half the difference of the measures of the intercepted arcs.
Interactive popup. Assistance may be required.
m ∠PZQ = 1 over 2 1 2 (mPQ – m
RS)RS)RSRS = 80.7° – 61.8°RS = 18.9°RS = 37.8°
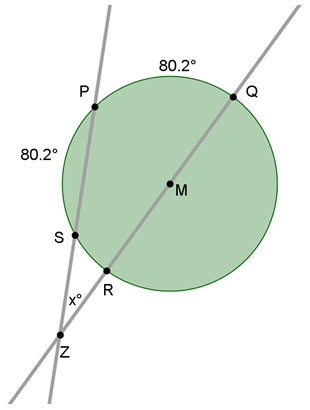
If QR is a diameter of the circle, what is the value of x, which represents the angle of intersection between the two sidewalks at point Z?
Interactive popup. Assistance may be required.
The measure of the angle between two secants that intersect outside a circle is one-half the difference of the measures of the intercepted arcs. Also, remember that the diameter of a circle intercepts a semicircle, which has an arc measure of 180°.
