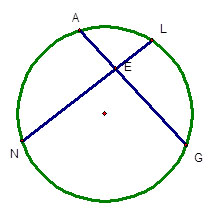
In this section, you will investigate the relationships among angles formed by intersecting chords and the arcs they intercept, as well as angles formed by secants that intersect inside a circle and the arcs they intercept.
In order to investigate this relationship, you will use an interactive applet pictured below. To use this applet, click and drag one of the 4 red points on the circle. As you move these points around, observe m
AN , m
LG , and m ∠AEN.
Click on the image below to open the applet. Manipulate the angle so that m∠AEN is close to 60 degrees, then 90 degrees, and finally 120 degrees.
Copy the table below into your notes, and then use the measures of the arcs for each of these angle measures to complete the table and answer the questions below.
| m ∠ AEN | m
AN |
m
LG |
m
AN + m
LG |
| 60° | |||
| 90° | |||
| 120° |
AN + m
LG ?
Interactive popup. Assistance may be required.
m∠AEN = 1 over 2 1 2 (mAN +m
LG)
AN and
LG are the intercepted arcs of the two chords, what can you say about the measure of the angle between two intersecting chords and the measures of the intercepted arcs?
Interactive popup. Assistance may be required.
If two chords intersect inside a circle, then the measure of the angle formed is equal to half the sum of the measures of the intercepted arcs.
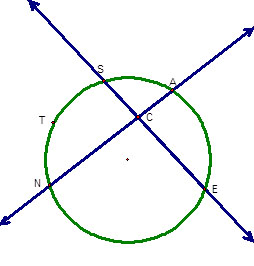
Recall that a chord is a line segment that has two endpoints on the circle, and a secant is a line that intersects the circle at two points. A chord is a line segment contained in a secant line. For example, in the diagram shown, the chord AN is contained in the secant
AN.
Let’s extend what you have seen about the angle between two intersecting chords to the angle between two intersecting secant lines. To do so, you will use the interactive applet pictured below. To manipulate this applet, click and drag point C and move it throughout the circle. Additionally, to move the secants, click and drag the red points on each secant found on the left side of the applet. As you move these points around, observe m
NTS , m
AE , and m∠ECA.
Click on the image below to open the applet. Manipulate the applet so that m∠ECA is close to 60 degrees, then 90 degrees, and finally 100 degrees.
Copy the table below into your notes, and then use the measures of the arcs for each of these angle measures to complete the table and answer the questions below.
| m ∠ ECA | m
NTS |
m
AE |
m
NTS + m
AE |
| 60° | |||
| 90° | |||
| 120° |
NTS + m
AE?
Interactive popup. Assistance may be required.
m ∠ECA = 1 over 2 1 2 (mNTS + m
AE)
NTS and
AE are the intercepted arcs of the two secants, what can you say about the measure of the angle between two intersecting secants and the measures of the intercepted arcs?
Interactive popup. Assistance may be required.
If two secants intersect inside a circle, then the measure of the angle formed is equal to half the sum of the measures of the intercepted arcs.
How does the relationship between the angle created by two intersecting chords and their intercepted arcs compare to the relationship between the angle created by two intersecting secants (inside a circle) and their intercepted arcs?
Interactive popup. Assistance may be required.
The relationships are the same. The measure of the angle created by the intersecting chords or secants is one-half the sum of the measures of the intercepted arcs created by the chords or secants.
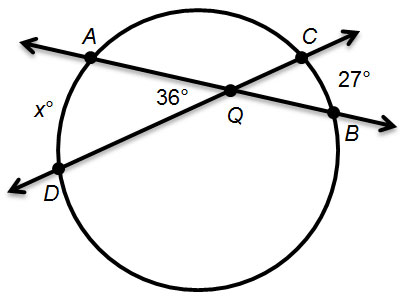
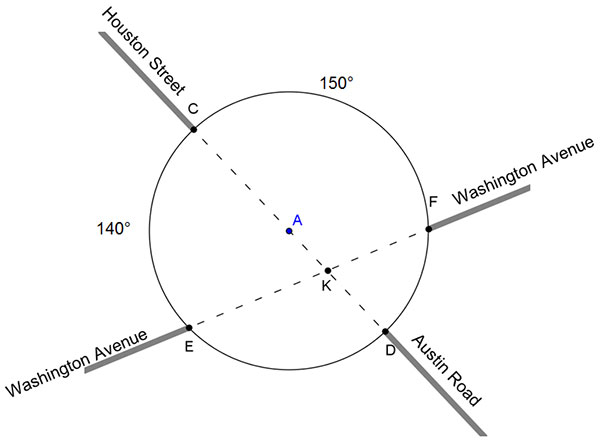
If Houston Street and Austin Road were connected, they would pass through the center of the circle. What is the angle between Washington Avenue and Austin Road, represented by ∠FKD in the diagram?
