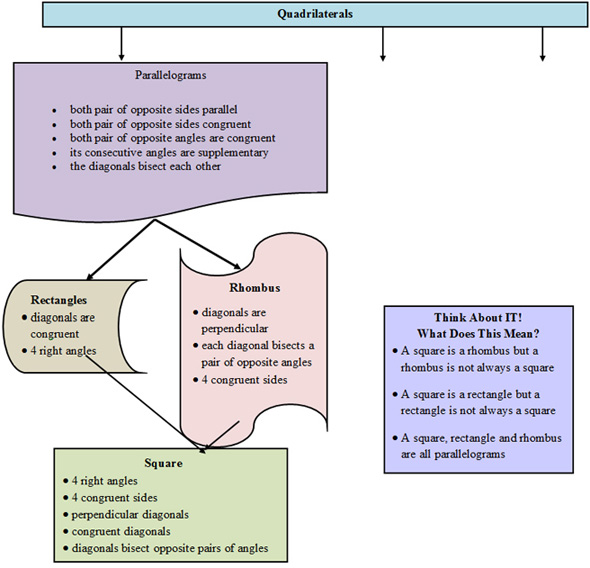
Finally, the last of the special parallelogram!

Let’s see where the square fits into this picture. By definition, a square is a quadrilateral with four right angles and four congruent sides.

• Did you notice that the rectangle has 4 right angles?
• Did you notice that the rhombus has 4 congruent sides?

That means that the square has all of the properties of a rhombus, a rectangle, and a parallelogram!

To sum it up, a square has all of the properties of a parallelogram, plus the following:

That means, I can start with a square which has properties of all of the other parallelograms, then go to the rectangle. If I stretch the square out at the sides, the diagonals are still congruent but they are no longer perpendicular.

Start the animation and watch as vertex B of square ABCD is dragged horizontally to make a rectangle.

In your notes, describe what happens to the diagonals when you change the figure from a square to a rectangle.

Click on the image below to launch a new applet that will allow you to compare relationships between the angles and diagonals of rectangles, squares, and rhombi:

Let’s add the square to the quadrilateral flow chart!