In the previous section, you investigated four important properties of parallelograms:

Theorem 1: If a quadrilateral is a parallelogram, then its opposite sides are congruent.
Theorem 2: If a quadrilateral is a parallelogram, then its opposite angles are congruent.
Theorem 3: If a quadrilateral is a parallelogram, then its consecutive angles are supplementary.
Theorem 4: If a quadrilateral is a parallelogram, then its diagonals bisect each other.


In this section, you will apply those theorems and properties to solve problems.

Theorem 2: If a quadrilateral is a parallelogram, then its opposite angles are congruent.

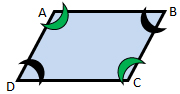
Look at the parallelogram to the right.
∠A and ∠C are opposite angles, therefore ∠A≅∠C
∠B and ∠D are opposite angles, therefore∠B≅∠D

If we know that the m∠D = 3x + 5 and m∠B = 4x - 15, we can find the measure of each angle. Since the angles are congruent, we know they have the same measure. We can set the two expressions equal and solve for x. Once we know the value of x, you can substitute the value of x into each expression to verify that the two angles have the same measure and are congruent.

4x - 15 = 3x + 5

4x - 15 + 15

3x+ 5 + 15

4x

3x + 20

4x - 3x

3x - 3x + 20

x

20

 

Check Your Answer

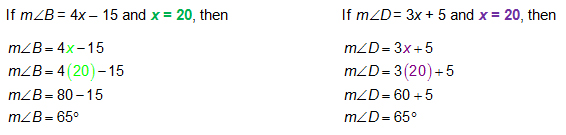
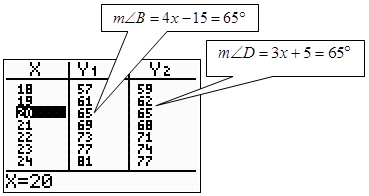
TIP: Check your answer using a graphing calculator:

  1. Open the function editor of your graphing calculator.
  2. Enter the expression on the left-hand side of the equals sign into Y1.
  3. Enter the expression on the right-hand side of the equals sign into Y2.
  4. Go to the table feature of your calculator.
  5. Scroll down the x-column until you see the same value in the row for the Y1 and Y2 columns.
  6. The x-value is the value of x, and the values in Y1 and Y2 tell you the measures of the two angles!

Image of calculator output showing a table where x equals 20 and the values in the y1 and y2 columns are both 65

You Try One!

Interactive exercise. Assistance may be required. Scroll your mouse pointer over each blank below to check your work:

Now you have the value of x, substitute this value into the expression that represents m∠K.

Just to Make Sure

Theorem 3: If a quadrilateral is a parallelogram, then its consecutive angles are supplementary.

Image shows parallelogram ABCD where A and B are consecutive angles

If you know that m∠A = 3x + 15and m∠B = 2x + 5, you can find the measure of each angle of the parallelogram.

m∠A + m∠B = 180o

Step 1  3x + 15 + 2x + 5 = 180
Step 2  5x + 20 = 180
Step 3  5x + 20 - 20 = 180 - 20
Step 4  5x = 160
Step 5   5x 5 160 5
Step 6  x = 32

You've Found the Value of x But You're Not Done Yet!

If m∠A = 3x + 15and x = 32, then:

m∠A = 3x + 15
m∠A = 3(32) + 15
m∠A = 96 + 15
m∠A = 111o

If m∠B = 2x + 5 and x = 32, then:

m∠B = 2x + 5
m∠B = 2(32) + 5
m∠B = 64 + 5
m∠B = 69o

Check Your Answer

You found the angle measures, but are they really supplementary? Let's check and be sure.

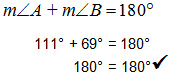
Theorem 4: If a quadrilateral is a parallelogram, then its diagonals bisect each other.

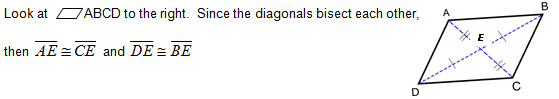
Image shows parallelogram ABCD with diagonals AC and BD intersecting at E

Source: Parallelogram, Wikimedia

If we know that AE = 3x - 5 and CE = x + 25, finding the length AC is a breeze.

Since the diagonals of a parallelogram bisect each other, we know that AE = CE. This of course means that 3x - 5 = x + 25. Let's solve for x and then find AC.

Interactive popup. Assistance may be required.

View the steps to solve for x

Close Pop Up

Now Try One On Your Own

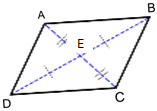
Image shows quadrilateral ABCD with diagonals AC and BD intersecting at E

ABCD is a quadrilateral. If AE = 2x - 1 and CE = x + 7, find the value of x so that ABCD is a parallelogram, then find AC.

Show all of your work in your notes.

Interactive popup. Assistance may be required.

Check Your Answer

x = 8, AC = 15

Did you remember to show your work?

Close Pop Up