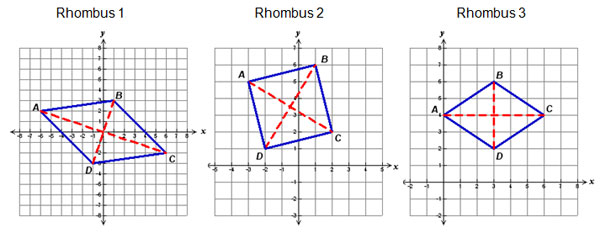
Below are graphs of three different rhombi with their diagonals marked and the following vertices:
On your own paper copy, and complete the table shown below finding the slopes of the diagonals of each rhombus.

| Slope of diagonal AC | Slope of diagonal BD | |
| Rhombus 1 | ||
| Rhombus 2 | ||
| Rhombus 3 |
Once you've created the table, you may Interactive popup. Assistance may be required.
| Slope of diagonal AC | Slope of diagonal BD | |
| Rhombus 1 | -
1
3
|
3 |
| Rhombus 2 | -
3
5
|
5
3
|
| Rhombus 3 | 0 |
undefined |

Based on the results of your data, what appears to always be true about the relationship between the slopes of the diagonals of a rhombus?
Rrecord your data in your notes.

If you were given only the coordinates of the vertices, how could you determine if a quadrilateral was a rhombus? Record your data.

Based on this experiment, look at the other quadrilaterals in this flow chart below. First, notice how the quadrilaterals are grouped. There are three sections below quadrilateral: parallelogram, kite, and trapezoid. Each grouping is a special quadrilateral of the one above it. Under parallelogram are rectangle, rhombus, and square. Below kite is a right kite and below the trapezoid are two special trapezoids: isosceles and right trapezoids. Which do you think would have slopes that are perpendicular to each other?
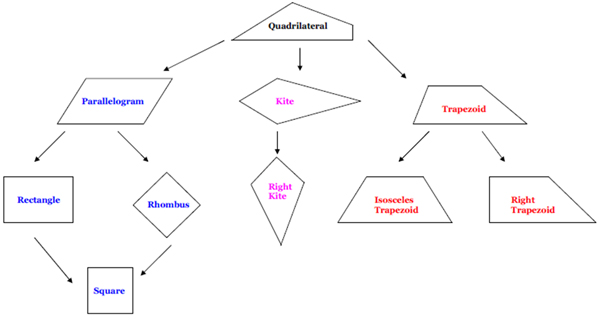
Source: Properties of Quadrilaterals, Mr. Besworth, Mayfield Secondary School
| Diagonals Perpendicular? Always, Sometimes, Never | Check Your Answer | |
| Quadrilateral | Interactive button. Assistance may be required. | |
| Parallelogram | Interactive button. Assistance may be required. | |
| Rectangle | Interactive button. Assistance may be required. | |
| Rhombus | Always | |
| Square | Interactive button. Assistance may be required. | |
| Kite | Interactive button. Assistance may be required. | |
| Right Kite | Interactive button. Assistance may be required. | |
| Trapezoid | Interactive button. Assistance may be required. | |
| Isosceles Trapezoid | Interactive button. Assistance may be required. | |
| Right Trapezoid | Interactive button. Assistance may be required. |
Given the following coordinates of the vertices of a quadrilateral, determine algebraically if the figure could be a rhombus.
Quadrilateral |
Vertex A |
Vertex B |
Vertex C |
Vertex D |
Rhombus? Possible/ Impossible |
Check Your Answer |
1 |
(2.5, 4) |
(2, 2) |
(4, 2.5) |
(4, 4) |
||
2 |
(1.5, 4.5) |
(2.5, 2) |
(3, 5) |
(5.5, 4) |
||
3 |
(1.5, 4.5) |
(1.5, 2.5) |
(4, 2) |
(3.5, 2) |
||
4 |
(-1, 2) |
(-2, 0) |
(-1, -2) |
(0, 0) |
What other element would you need to show the above "possible" rhombi are in fact rhombi?