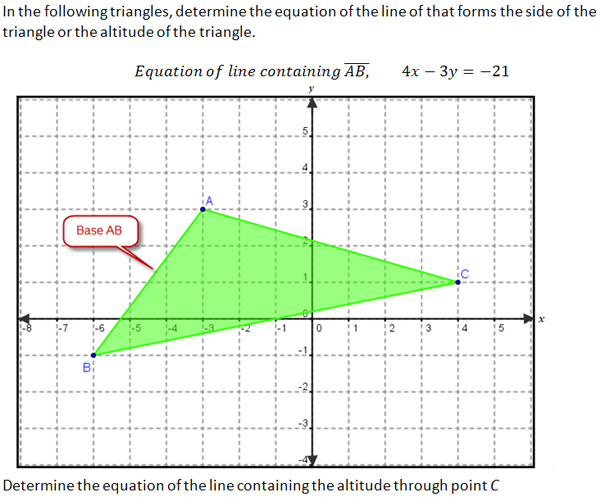
In this lesson, you will explore figures on the coordinate plane by using what you know about special lines/segments in triangles and polygons to determine their algebraic relationship. It would be helpful to have completed the lesson Parallel and Perpendicular Lines prior to this lesson, which is module 3, lesson 7.

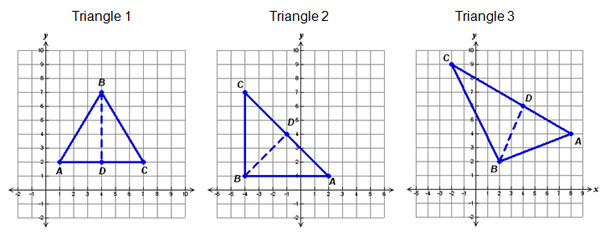
Below are graphs of three different triangles and their altitudes. The vertices of the base and the altitudes are listed below:

• Triangle 1 – A (1,2), C (7,2), and B (4,7), D (4,2)
• Triangle 2 - A (2,1), C (-4,7), and B (-4,7), D (-1,4)
• Triangle 3 - A (8,4), C (-2,9), and B (2,2), D (4,7)

On your own paper copy, and complete the table shown below finding the slopes of the base and altitude of each triangle.

Interactive popup. Assistance may be required.

Click here to check your answer.

	Slope of base AC	Slope of altitude BD
Triangle 1	0	Undefined
Triangle 2	-1	1
Triangle 3	- 1 2	2

Based on the results of your data, what appears to always be true about the relationship between the slope of an altitude and its corresponding base?

Record your data in your notes. Interactive popup. Assistance may be required. Click here to check your answer. The slopes are negative reciprocals, which makes the altitude always perpendicular to the base.

Answer the following two problems on your own paper.

y = - three-fourths 3 4 x + 4

Interactive popup. Assistance may be required.

Click here to check your answer.

y = 3x - 10