Now that you have solid understating of graphing lines that are parallel and perpendicular, solve the following situation using a coordinate grid.

Use the Cool Math online calculator or your own graphing calculator to graph the following designs made with linear equations.

Graphing Calculator

1. Thomas had $40 in his savings account at the beginner of the summer. His neighbor offered him $35 to mow his lawn each week during the summer.  Thomas decided to deposit $20 of the $35 each week to build up his savings.  
1. What equation would model Thomas’ situation?
2. How much money would Thomas have in his savings account after 15 weeks?
3. How many weeks would Thomas need to save at his current rate to buy a new cell phone that cost $345.00?
Interactive popup. Assistance may be required.
Check Your Answer
1. y = 20x + 40
2. $340
3. At least 16 weeks.


2. Jasmine owed her brother $40 at the beginning of the summer.  Her neighbor also offered her $35 to mow his lawn each week during the summer.  Jasmine also wanted to save $20 each week to build up her savings.
1. What equation would model Jasmine’s situation?
2. How much money would Jasmine have in her savings account after 15 weeks?
3. If Jasmine wanted to purchase the same cell phone as Thomas, how many weeks would it take her to save it?
4. How do the graphs for the models of Thomas’ savings and Jasmine’s savings compare?
5. How do the equations for the models of Thomas’ savings and Jasmine’s savings compare?
6. How did you use the graph to determine the answers to the questions above?
Interactive popup. Assistance may be required.
Check Your Answer
1. y = 20x - 40
2. $260
3. At least 20 weeks.
4. They are parallel lines.
5. They have the same slope of 20 but different y-intercepts.
6. The x-axis represented the number of weeks mowed and the y-axis represented the amount in the savings account. So, for instance, the coordinate (15, 340) showed 15 weeks of mowing and $340 in savings.


3. Money spent on medical research is increasing each year. The graph below compares the amount spent on cancer research to the amount spent on heart disease research since 1992.



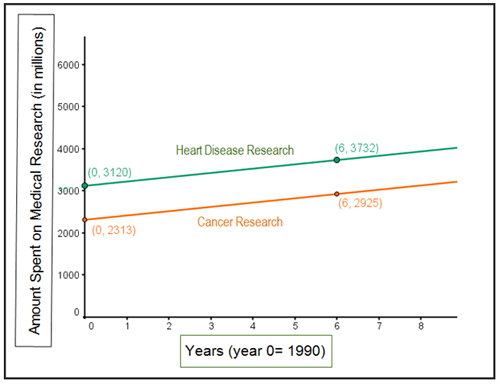
1.  Find the equation of the each line that models the research dollars spent.

Cancer Research____________
Heart Disease Research __________

2. What is the rate of change spent on spent on the research?

Cancer Research____________
Heart Disease Research __________

3. Use the equations to predict the amount that will be spent in the year 2020 if spending continues at the current rates.

Cancer Research____________
Heart Disease Research __________

4. How do the two graphs compare?
5. According to the model, is there a time when the amount of spending for both types of research be the same?
Interactive popup. Assistance may be required.
Check Your Answer
1. Cancer Research   y = 102x + 2313
   Heart Disease Research   y = 102x + 3120
2. Cancer Research  102 million
   Heart Disease Research 102 million
3. Cancer Research   6,373 million
   Heart Disease Research 7,180 million
4. The two lines are parallel.
5. E. If the rates stay the same, the money for heart disease research will always be more than the money for cancer research.


4. Many times in mathematics, we are asked to find equations.  Using the information in the graph below, find the equation of the line given. Then, find the equations of the lines that are parallel to and perpendicular to the given line which passes through the point (0, 9).



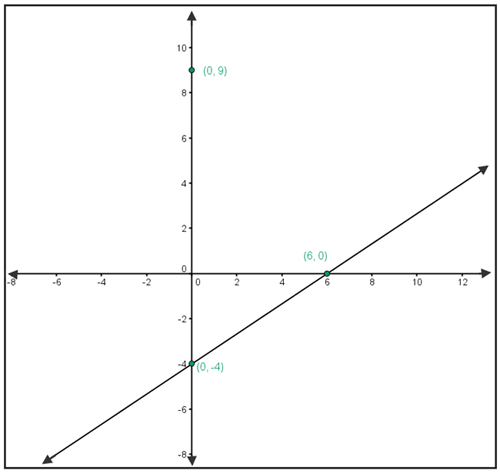
1. Original line____________________
2. Parallel to the original through (0,9)____________________
3. Perpendicular to the original through (0,9)____________________
4. How does the original line compare to the parallel line?
5. How does the perpendicular line compare to the original?
Interactive popup. Assistance may be required.
Check Your Answer
1. Original lines y = (2/3)x - 4
2. Parallel to the original y = (2/3)x + 9
3. Perpendicular to the original y = -(3/2)x + 9
4. Their slopes are the same.
5. Their slopes are negative reciprocals of each other.