In this section, you will use nets to determine the surface area of a given figure.

Part 1: Surface Area of Cones

Let’s use the net of a cone to help us measure and describe three-dimensional figures in terms of exterior (surface area) and capacity (volume).

Based on the net of the cone that we looked at in the previous section, let’s see how the net can help derive the formula to find the surface area for the cone.

Video segment. Assistance may be required. The video below shows the source of the formula for the surface area of a cone and how it relates to the net of the cone.


*The reference in this video to the state assessment is outdated.

Find the total surface area of the net of a cone with the height of four centimeters and a radius of three centimeters. Compare your work with the student work sample below.

Geometry Solutions

Part II: Surface Area of Prisms

Finding the surface area of a prism from its net is not as difficult as using the net of a cone.

China's National Aquatic Centre or "Water Cube" that was used in the 2008 Beijing Olympics serves as a good example. Although the building itself is a complex hexahedron, the net of a rectangular prism can be helpful in determining the surface area of the building.

Interactive exercise. Assistance may be required. Click the Start Animation button below to view the animation. Once the animation is complete, you can replay it by clicking the Replay Animation button.

Given the approximate dimensions in the net of the Water Cube, what is the surface area of the exposed faces (faces that you would see if you were looking at the actual building)?

Interactive popup. Assistance may be required.

Check Your Answer

(176 × 176) + 4(176 × 31) = 52,800 m2Close Pop Up

Pause and Reflect

How does a net help you to determine the surface area of a three-dimensional figure?

Interactive popup. Assistance may be required.

Check Your Answer

The net makes it easier to see the faces or surfaces of the figure, which in turn helps you to identify the dimensions and formulas that are necessary to calculate the surface area.Close Pop Up

Practice

Determine the surface area of each of the figures represented by the nets shown below.


  1. Interactive popup. Assistance may be required.

    Need a hint?

    What shapes are present in the net? What are the area formulas for those shapes?Close Pop Up

    Interactive popup. Assistance may be required.

    Check Your Answer

    The figure is a triangular prism, so determine the area of the 2 congruent triangular bases and the area of the 3 rectangular lateral faces.
    Area of base:
    A = 1 over 2 1 2 bh
    A = 1 over 2 1 2 (3.5 cm)(5 cm)
    A = 8.75 cm2    		 Area of lateral face:

    A = bh
    A = (3.5 cm)(20 cm)
    A = 70 cm2
    Total surface area = 2 × 8.75 cm2 + 3 × 70 cm2 = 227.5 cm2
    Close Pop Up


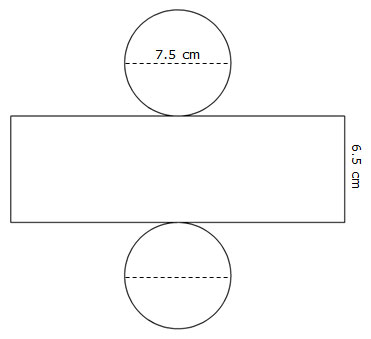
  2. Interactive popup. Assistance may be required.

    Need a hint?

    What shapes are present in the net? What are the area formulas for those shapes?Close Pop Up

    Interactive popup. Assistance may be required.

    Check Your Answer

    The figure is a cylinder, so determine the area of the two congruent circular bases and the area of the rectangular lateral surface.
    Area of base:
    A = πr2
    A = π(3.75 cm)2
    A ≈ 44.16 cm2    		 Area of lateral face:
    A = bh
    A = ((7.5 cm)(π))(6.5 cm)
    A ≈ (23.55 cm)(6.5 cm)
    A ≈ 153.08 cm2
    Total surface area = 2 × 44.16 cm2 + 153.08 cm2 = 241.4 cm2
    Close Pop Up