Although Euler's Theorem does not apply when describing the attributes of the nets of cylinders and cones, there are some special relationships. However, these relationships will become more apparent once you begin to use nets in the application of measuring solids.
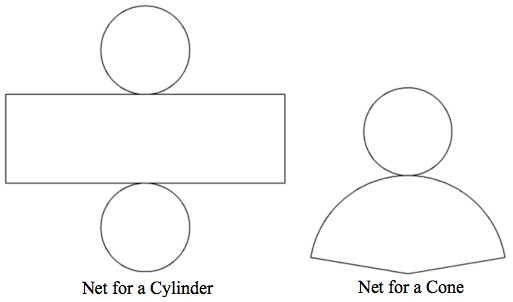
Study the nets for a cylinder and a cone shown above. Use the diagrams to determine the appropriate word for each blank describing the attribute of each net. Use the dropdown menus to select the appropriate word.
Interactive popup. Assistance may be required.
What shape(s) appear in both nets?
Interactive popup. Assistance may be required.
Both nets contain one or more circles.
Interactive popup. Assistance may be required.
A polygon is a flat shape that is a closed figure and contains no curved sides.
Interactive popup. Assistance may be required.
No, because the nets contain circles and a sector of a circle, and these figures contain curved edges, so they cannot be polygons.
Interactive popup. Assistance may be required.
A polygon is a flat shape that is a closed figure and contains no curved sides.
Interactive popup. Assistance may be required.
No, because a surface must be a polygon in order to be a face, and these surfaces are not faces.
An edge is the intersection of two or more faces, and a vertex is the intersection of two or more edges. Do cylinders or cones have edges and vertices? How do you know?
Interactive popup. Assistance may be required.
No. Because none of the surfaces of cylinders or cones are polygons, they cannot be faces. Since there are no faces, there cannot be edges. Since there are no edges, there cannot be vertices.
The peak of a cone is sometimes called an apex or a vertex of the cone. How is this vertex like vertices in polyhedra? How is it different?
Interactive popup. Assistance may be required.
The vertex of a cone is like a vertex of a polyhedron in that it is a point along the outside of the three-dimensional figure. It is different because there are no defined edges that intersect to create the vertex. In fact, it appears as though there are an infinite number of edges that intersect to create the vertex of a cone.