
Source: Leonhard Euler, Jakob Emmanuel Handmann, Wikimedia Commons
Although polyhedra are generally named by the number of faces that make up the figure, it is common to see qualifier of the face shape within the name.
Likewise, in naming three-dimensional figures that are not regular polyhedron, it is critical to know the shape of the base. The name of the shape of the base will be used in naming the solid and the net of the solid.

Source: Leonhard Euler, Jakob Emmanuel Handmann, Wikimedia Commons
Euler’s Theorem tells us the relationship between the number of faces, edges, and vertices in any polyhedron. Remember that a polyhedron is a three-dimensional figure whose faces are all polygons, and polygons are planar shapes with closed edges and no curved edges.

Will Euler’s Theorem still apply to a polyhedron that is not regular?
 |
 |
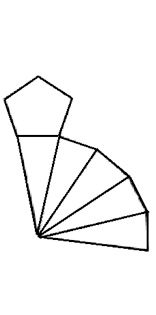 |
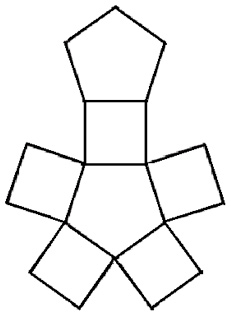
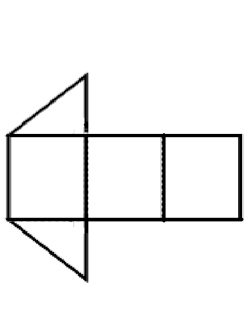
Look at the table below to see information about each polyhedron.
| Name of Shape | Number of Vertices | Number of Faces | Number of Edges | Check V+F – E = 2 |
| Pentagonal Prism | 10 |
7 |
15 |
10 + 7 – 15 = 2 |
| Triangular Prism | 6 |
5 |
9 |
6 + 5 – 9 = 2 |
| Pentagonal Prism | 6 |
6 |
10 |
6 + 6 – 10 = 2 |
Interactive popup. Assistance may be required.
How are regular polyhedra different from the 3 polyhedra that you investigated in the applet?
Interactive popup. Assistance may be required.
Although these nets do not fold into regular polyhedra, they are still polyhedra. The relationship that is expressed in Euler’s Theorem is regarding the relationship of polygons that create the polyhedron. Even though the orientation of the shape may change, as seen by the nets, the attributes and characteristics of the shape do not.
Interactive popup. Assistance may be required.
What three-dimensional figures can you think of that are not composed entirely of faces that are polygons?
Interactive popup. Assistance may be required.
Euler’s Theorem will not apply to nets of cylinders and cones because the shapes in the nets themselves are not polyhedra, meaning they are not formed by polygons.
How does using a net help you to visually recognize faces, edges, and vertices of a three-dimensional figure?

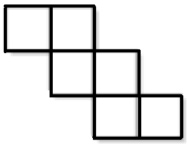
Interactive popup. Assistance may be required.
How many faces are present in the net? What shapes are the faces?
Interactive popup. Assistance may be required.
Cube
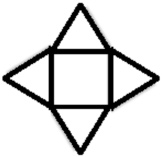
Interactive popup. Assistance may be required.
How many faces are present in the net? What shapes are the faces?
Interactive popup. Assistance may be required.
Name of Solid: square pyramid
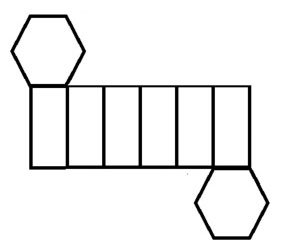
How many faces, edges, and vertices does the three-dimensional figure represented by the net have?
Interactive popup. Assistance may be required.
What type of figure is represented by the net?
Interactive popup. Assistance may be required.
Number of Faces: 8