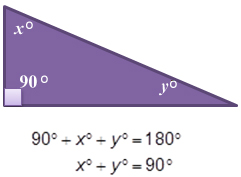
Since x and y are both positive numbers:
x < 90° and y < 90°
So x and y are both measures of acute angles!
The Pythagorean Theorem is used to determine the length of one side of a right triangle when the lengths of the other two sides of the right triangle are known. For more information about the Pythagorean Theorem, please visit one of the reference links of this resource.
Right triangles are used by designers, architects, and engineers to solve a multitude of problems. Mechanical and civil engineers, for example, use right triangles to help design and build bridges that distribute the weight load evenly over a point, making it possible to connect remote places. Strategic bridges, such as the Golden Gate bridge in San Francisco, the Verrazano Narrows bridge in New York City, or the Fred Hartman bridge in Houston, make commerce possible by enabling drivers to cross bodies of water. These bridges serve as shortcuts saving millions, if not billions, of dollars each year.
In this resource, you will investigate patterns that are found in special right triangles. These special right triangles have properties by virtues of the measures of their acute angles.
Recall that any right triangle must contain two acute angles. Otherwise, the sum of the measures of the interior angles would be greater than 180°, and then it wouldn’t be a triangle!
 |
Since x and y are both positive numbers: x < 90° and y < 90° So x and y are both measures of acute angles! |
![]() The first special right triangle that we will investigate is created from an equilateral triangle.
The first special right triangle that we will investigate is created from an equilateral triangle.
Let’s use a 30°-60°-90° triangle with a shorter leg length of 1 unit to look for relationships among the lengths of the three sides of the triangle.
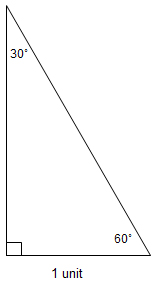
Fold the 60° angle in half so that the shorter leg lines up over the hypotenuse.
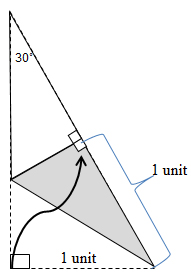
What is the measure of the new angle that you created when you folded the 60° in half? How do you know?

The 1 unit leg now touches the hypotenuse of the original right triangle. Fold the original 30° angle on top of the new 30° as shown.

What happened to the hypotenuse of your original triangle when you folded the 30° angles on top of one another?
How does the length of the original hypotenuse compare to the length of the original shorter leg? How do you know?

If the length of the original leg (which has now been folded on top of the original hypotenuse) is 1 unit, what is the length of the original hypotenuse?
![]() Now, use the Pythagorean Theorem to find the length of the remaining side of your original triangle.
Now, use the Pythagorean Theorem to find the length of the remaining side of your original triangle.
![]() Fill in the a chart like the one below to summarize your findings. You may make this chart in your notes. (You can check your work by moving your mouse over the question marks.)
Fill in the a chart like the one below to summarize your findings. You may make this chart in your notes. (You can check your work by moving your mouse over the question marks.)