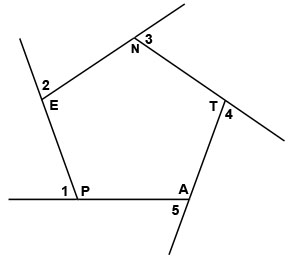
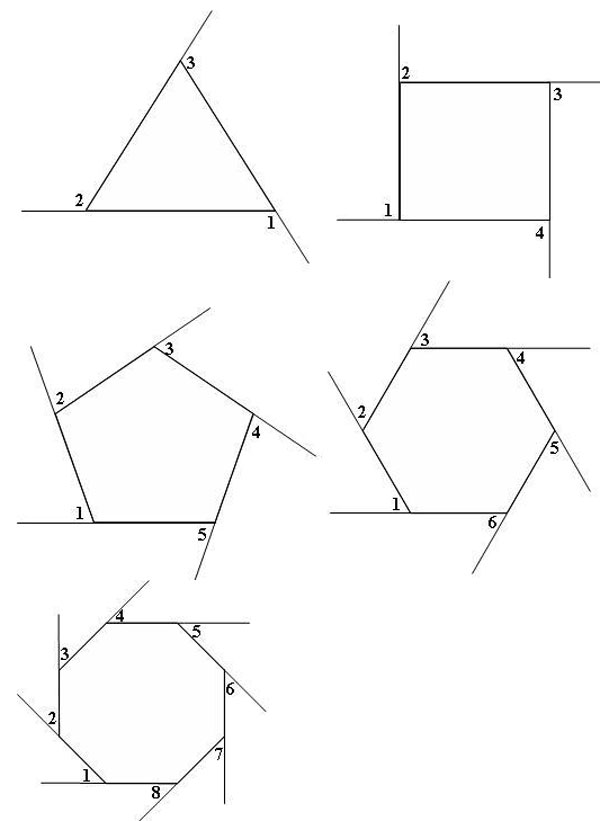
In this section, the equation to find the degree measure of an exterior angle of a regular polygon will be discovered. The use of a calculator is helpful but not necessary.
Answer the following questions.
| Polygon |
Number of Angles |
Sum of Interior Angles (total degrees in interior angles) |
Number of Degrees in Each Interior Angle |
Number of Degrees in Each Exterior Angle |
Sum of Exterior Angles |
| Triangle |
Interactive button. Assistance may be required.
_____
3 |
Interactive button. Assistance may be required.
_____
180 |
Interactive button. Assistance may be required.
_____
60 |
Interactive button. Assistance may be required.
_____
120 |
|
| Quadrilateral |
Interactive button. Assistance may be required.
_____
4 |
Interactive button. Assistance may be required.
_____
360 |
Interactive button. Assistance may be required.
_____
90 |
Interactive button. Assistance may be required.
_____
90 |
|
| Pentagon |
Interactive button. Assistance may be required.
_____
5 |
Interactive button. Assistance may be required.
_____
540 |
Interactive button. Assistance may be required.
_____
108 |
Interactive button. Assistance may be required.
_____
72 |
|
| Hexagon |
Interactive button. Assistance may be required.
_____
6 |
Interactive button. Assistance may be required.
_____
720 |
Interactive button. Assistance may be required.
_____
720 |
Interactive button. Assistance may be required.
_____
60 |
|
| Octagon |
Interactive button. Assistance may be required.
_____
8 |
Interactive button. Assistance may be required.
_____
1080 |
Interactive button. Assistance may be required.
_____
135 |
Interactive button. Assistance may be required.
_____
45 |
|
| n-gon - is a polygon with n number of sides |
Interactive button. Assistance may be required.
_____
n |
|
|
|
Interactive button. Assistance may be required.
_____
360
|
Use the figures above to assist in completing the chart above to discover the equation for the degree or measure of an exterior angle of a regular polygon.
Answer the following questions.