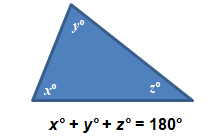
Recall that the sum of the measures of the interior angles of any triangle is 180°.

In this section, you will find the sum of the measures of the interior angles of other polygons and then develop an algebraic representation for the sum of the measures of the interior angles of any polygon.

In your notes, create a table like the one below.

Complete the table by first drawing all possible diagonals from one vertex of each polygon and then filling in the columns that follow. The first two are partially done for you.

Check your responses by moving your mouse over the blanks.

Use your notes and the table above to answer the following questions.

1. Write a function rule, S(n), that expresses the relationship between the number of sides, n, of a polygon and the sum of the interior angles.
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   S(n) = 180(n-2) or S(n) = 180n - 360
   
   
   
2. Use your graphing calculator to create a scatterplot of sum of interior angles vs. number of sides, and check your function rule by graphing it over your scatterplot.
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   
   
   
   
3. What is the sum of the interior angles of a dodecagon (12 sides)?
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   A dodecagon has 12 sides, so S(n) = 180(12-2) = 180(10) = 1800°
   
   
   
4. If the sum of the interior angles of a polygon is 3060°, how many sides does the polygon have?
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   Since we know the sum, substitute it in for S(n) and solve for n.

   3060 = 180(n − 2)

   3060 over 180 3060 180 = 180 (n minus 2) over 180 180 (n − 2) 180 So the polygon has 19 sides.

   17 = n − 2

   n = 19

   
   
   
   
5. It is impossible to have a sum of 2400° for the interior angles of a convex polygon. Explain why.
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   If we substitute 2400° in for S(n) and solve for n, we get:

   2400 = 180(n − 2)

   2400 over 180 2400 180 = 180 (n minus 2) over 180 180 (n − 2) 180

   13.3 = n − 2

   n = 15.3

   But it is not possible to have a polygon with 15.3 sides. Therefore, it's not possible to have a sum of interior angles of 2400°.