In this section, you will investigate relationships of the scale factor in similar cones.

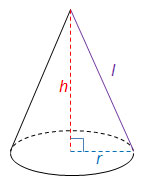
The animation below shows the relationship between the radius, height, and slant height of a cone. In the diagram below, h represents the height of the cone, r represents the radius, and l represents the slant height.

• If two segment lengths are known on a right circular cone, how can you find the third?

  Interactive popup. Assistance may be required.

  Need a hint?

  What polygon is formed by the radius, height, and slant height of a cone?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Use the Pythagorean Theorem.

• What information do you need to know in order to be sure that two right circular cones are similar?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The radii and the heights need to be proportional.

Cones A, B, C, D, and E are similar. One of the cones is shown in the diagram. Some of their lengths are given in the table. Complete the drag and drop puzzle to fill in the table. Drag the appropriate number to its correct place in the table. Click the Reset button if you need to reset the interactive.

• Do these ratios hold true for all 5 cones?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Yes

• Is more information needed to show that these cones are similar?

  Interactive popup. Assistance may be required.

  Check Your Answer

  No

Now, let’s look more closely at the volumes of similar cones. The volumes of three similar cones are shown below. Click on each volume to see how the volume was calculated.

Volume of Cone A (cubic units)	Volume of Cone B (cubic units)	Volume of Cone C (cubic units)
Interactive popup. Assistance may be required. 16π V = one-third 1 3 πr2h    = one-third 1 3 π(4)2(3)    = one-third 1 3 π(16)(3)    = 16π	Interactive popup. Assistance may be required. 128π V = one-third 1 3 πr2h    = one-third 1 3 π(8)2(6)    = one-third 1 3 π(64)(6)    = 128π	Interactive popup. Assistance may be required. 432π V = one-third 1 3 πr2h    = one-third 1 3 π(12)2(9)    = one-third 1 3 π(144)(9)    = 432π

Investigate volume relationships by completing the following drag and drop puzzle. Use the information in the volume calculations above to help you. Drag the appropriate tiles to the correct place on the table. Click the Reset button if you need to reset the interactive.

Use the information in the table you just completed to answer the following questions.

• How does the ratio of the corresponding lengths relate to the scale factor relating the similar cones?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The ratio of the corresponding lengths is equal to the scale factor.

• What is the relationship between the ratio of the volumes and the scale factor?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The ratio of the volumes is the cube of the scale factor.

• Without computing the volume of Cone D and Cone E, what do you expect the ratio of the volume of Cone D to Cone A will be? Cone E to Cone A?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Ratio of the volume of Cone D to Cone A 64:1 = 4³:1³
  Ratio of the volume of Cone E to Cone A 125:1 = 5³:1³

Pause and Reflect

How could you generalize the relationship between the scale factor z of two similar cones and the ratios of the volumes of those cones?

Interactive popup. Assistance may be required.

Check Your Answer

If the scale factor between two similar cones is z, then volume of the second cone will be increased or decreased by a factor of z³.

---

Practice

1. A manufacturer makes a snow cone cup that has a volume of 125 cubic centimeters. If the dimensions of the snow cone cup are all multiplied by a factor of 2.5 to make a larger snow cone cup, what is the ratio of the volume of the larger snow cone cup to the original snow cone cup?

   Interactive popup. Assistance may be required.

   Need a hint?

   How is the ratio of the volumes of two similar cones related to the scale factor between the dimensions of the similar cones?

   Interactive popup. Assistance may be required.

   Check Your Answer

   2.5³ : 1 = 15.625 : 1

2. Two similar cones are shown below.
   

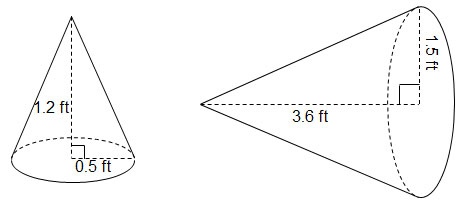
   What is the ratio of the volumes of the two cones?

   Interactive popup. Assistance may be required.

   Need a hint?

   How is the ratio of the volumes of two similar cones related to the scale factor between the dimensions of the similar cones?

   Interactive popup. Assistance may be required.

   Check Your Answer

   1:3³ : 1 = 1:27 : 1

3. Two similar cones have dimensions related by a scale factor of 2k. If the volume of the smaller cone is 15 cubic inches, what is the volume of the larger cone?

   Interactive popup. Assistance may be required.

   Need a hint?

   How is the ratio of the volumes of two similar cones related to the scale factor between the dimensions of the similar cones?

   Interactive popup. Assistance may be required.

   Check Your Answer

   15 × (2k)³ = 15 × (8k³) = 120k³