In this section, you will extend what you have seen so far with side lengths and areas of similar triangles to similar rectangles. In particular, you will examine patterns in perimeters and areas of similar rectangles.

Click on the image below to open the activity. Click on the orange points to adjust the dimensions of Rectangle A and the scale factor (using the slider). Click the Graphs button to see graphs of the relationships, and click the Measures button to see the measures and ratios with length, perimeter, and area of the two similar rectangles. Use the interactive and your explorations within the interactive to complete the table beneath the image.

Copy and complete the table comparing the ratios of the lengths of the given sides of the rectangles above in your notes.

Interactive popup. Assistance may be required.

Check Your Answer

Length of Rectangle A	Width of Rectangle A	Scale Factor	L' over L L' L = W' over W W' W	Perimeter of A over Perimeter of B Perimeter of A Perimeter of B	Perimeter of A over Perimeter of B Area of A Area of B
194	120	1.50	1.50	1.50	2.25
168	67	1.50	1.50	1.50	2.25
150	80	2.00	2.00	2.00	4.00
85	100	2.00	2.00	2.00	4.00

• What do you notice about the relationship between the scale factors and the ratios of the lengths of corresponding sides?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The scale factor is equal to the ratio of the lengths of corresponding sides.

• What do you notice about the relationship between the scale factors and the ratios of the perimeters?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The scale factor is equal to the ratio of the perimeters.

• What do you notice about the relationship between the scale factors and the ratios of the areas?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The ratio of the areas is equal to the square of the scale factor.

• What do you notice about the relationship between the ratios of the lengths of corresponding sides and the ratios of the areas?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The ratio of the areas is equal to the square of the ratios of the lengths of corresponding sides.

• Look at the graph of the Perimeter B/A versus Scale Factor. What function do you think models this relationship (hint: linear, quadratic, or exponential)? Why do you think that is the case?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The relationship could be modeled by a quadratic function because area is a two-dimensional measure.

• Look at the graph of the Area B/A versus Scale Factor. What function do you think models this relationship (linear, quadratic, or exponential)? Why do you think that is the case?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The relationship could be modeled by a quadratic function because area is a quadratic, or square, measure.

Pause and Reflect

If the scale factor is between 0 and 1, the dilation of the original rectangle would be a reduction instead of an enlargement. Do you think the same patterns between scale factor and ratio of perimeters and scale factor and ratio of areas would hold true? Use the interactive sketch to confirm your prediction.

Interactive popup. Assistance may be required.

Check Your Answer

Yes, the same patterns are true.

Practice

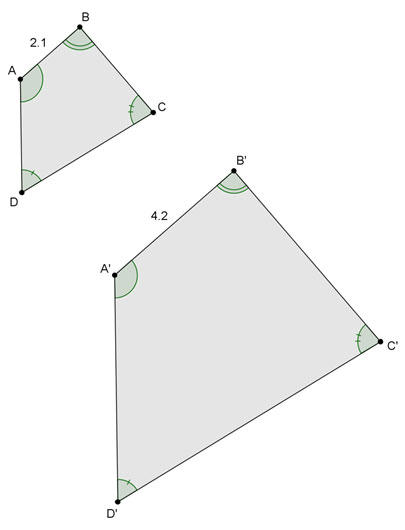
Use the two similar quadrilaterals shown in the figure below to answer questions 1-3.

1. If BC = 3.5 centimeters, what is B'C'? How do you know?

   Interactive popup. Assistance may be required.

   Need a hint?

   What is the ratio between the lengths of the two labeled corresponding sides?

   Interactive popup. Assistance may be required.

   Check Your Answer

   B'C' = 7 centimeters
   The scale factor generating A'B'C'D' from ABCD is equal to the ratio of the labeled corresponding sides, which is 2.
   B'C' = BC × 2 = 3.5 centimeters × 2 = 7 centimeters

2. What can you say about the ratio of the perimeters of A'B'C'D' and ABCD?

   Interactive popup. Assistance may be required.

   Need a hint?

   How does the ratio of the perimeters of similar figures compare to the ratio of the lengths of corresponding sides?

   Interactive popup. Assistance may be required.

   Check Your Answer

   The ratio of the perimeters is equal to the ratio of the lengths of the corresponding sides, which is equal to 2.

3. What can you say about the ratio of the areas of A'B'C'D' and ABCD?

   Interactive popup. Assistance may be required.

   Need a hint?

   How does the ratio of the perimeters of similar figures compare to the ratio of the lengths of corresponding sides?

   Interactive popup. Assistance may be required.

   Check Your Answer

   The ratio of the areas is equal to the square of the ratio of the lengths of the corresponding sides. The ratio of the areas is equal to 4.