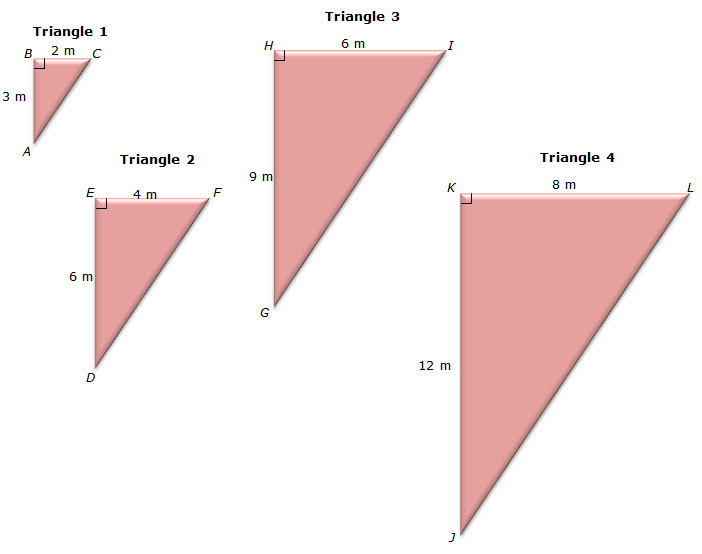
In this section, you will investigate the relationship between ratios of the scale factor and areas of similar triangles. Below is the same geometric pattern found in Section 1.

Using the information in the figure, complete the table. Enter your answers as ratios in lowest terms using colons (e.g., 4:1 represents a ratio of 4 to 1). The box will turn red if your answer is incorrect. You will use the completed table to answer the conclusion questions that follow.

Conclusion Questions

• How do the ratios of the areas compare to the ratios of the corresponding side lengths?

  Interactive popup. Assistance may be required.

  Need a hint?

  What patterns do you notice in the first numbers in the area ratios?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The ratios of the areas are the squares of the ratios of the corresponding sides.

• Use this relationship to predict the ratio of the area of Triangle 7 in the sequence to the area of ΔABC, where the ratio of the side lengths would be 7:1.

  Interactive popup. Assistance may be required.

  Need a hint?

  What is 7²?

  Interactive popup. Assistance may be required.

  Check Your Answer

  49:1

• Write an expression that could be used to determine the ratio of the area of Triangle n in the sequence to the area of ΔABC.

  Interactive popup. Assistance may be required.

  Need a hint?

  What pattern do you observe in the ratios of the areas?

  Interactive popup. Assistance may be required.

  Check Your Answer

  n²:1

• If the ratio of the area of a triangle to the area of ΔABC is 225:1, what would be the ratio of the lengths of the corresponding sides?

  Interactive popup. Assistance may be required.

  Need a hint?

  What is the inverse operation of squaring a number?

  Interactive popup. Assistance may be required.

  Check Your Answer

  15:1, since √225 = 15

• If the ratio of the corresponding side lengths is 2 over 3 2 3 :1, what would be the ratio of the area of the triangle to the area of ΔABC?

  Interactive popup. Assistance may be required.

  Need a hint?

  Apply your rule from the previous question to the ratio 2 over 3 2 3 :1.

  Interactive popup. Assistance may be required.

  Check Your Answer

  4 over 9 4 9 :1

Pause and Reflect

If you have similar quadrilaterals, how do you think the ratios of their areas would compare to the ratios of the lengths of the corresponding sides?

Interactive popup. Assistance may be required.

Check Your Answer

The area ratios would still be the square of the ratios of the lengths of the corresponding sides for similar quadrilaterals.

Practice

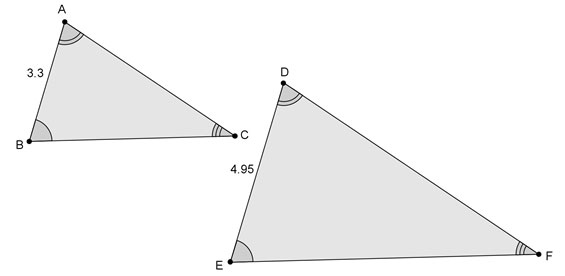
Use the similar triangles shown below to answer questions 1 and 2.

1. If the perimeter of ΔABC is 17 units, what is the perimeter of ΔDEF?

   Interactive popup. Assistance may be required.

   Need a hint?

   How do you determine the perimeter of a triangle?
   Interactive popup. Assistance may be required.

   Check Your Answer

   Perimeters of similar figures have the same ratios as the lengths of their corresponding sides.
   
   AB over DE AB DE = AB over DE P(ΔABC) P(ΔDEF)
   
   3.3 over 4.95 3.3 4.95 = 17 over x 17 x
   
   x = 25.5
2. What is the ratio of the area of ΔDEF to the area of ΔABC?

   Interactive popup. Assistance may be required.

   Need a hint?

   What is the ratio of the lengths of the corresponding sides?
   Interactive popup. Assistance may be required.

   Check Your Answer