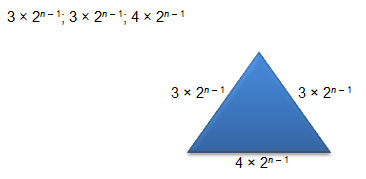Use the interactive below to create a sequence of similar triangles. Use the results from the interactive to complete the table that follows and answer the questions.

Copy and complete the table comparing the ratios of the lengths of the given sides of the triangles above into your notes or onto your own sheet of paper.

Interactive popup. Assistance may be required.

Check Your Answer

Original Segment	ΔDEF	ΔGHI	ΔJKL
AB	DE over AB DE AB = 6 over 3 6 3 = 2	GH over AB GH AB = 9 over 3 9 3 = 3	JK over AB JK AB = 12 over 3 12 3 = 4
BC	EF over BC EF BC = 4 over 2 4 2 = 2	HI over BC HI BC = 6 over 2 6 2 = 3	KL over BC KL BC = 8 over 2 8 2 = 4

Conclusion Questions

• What do you notice about the ratios of each pair corresponding sides for each triangle as compared to the original triangle ΔABC?

  Interactive popup. Assistance may be required.

  Need a hint?

  What patterns do you notice within each column?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The ratios of each pair of corresponding sides for each triangle as compared to ΔABC are equal.

• What do you notice about the included angle between each pair of corresponding sides?

  Interactive popup. Assistance may be required.

  Need a hint?

  An included angle is the angle between two sides of the triangle.

  Interactive popup. Assistance may be required.

  Check Your Answer

  The included angles have the same measure.

• Which similarity theorem shows that the triangles are similar? How do you know?

  Interactive popup. Assistance may be required.

  Need a hint?

  What information do you have about corresponding sides and corresponding angles?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The given corresponding sides are in proportion and since the sides are in proportion and the included angle is a right angle, and all right angles are congruent. This satisfies SAS Similarity Theorem.

• How does the scale factor used to generate each triangle compare to the triangle number in the sequence?

  Interactive popup. Assistance may be required.

  Need a hint?

  The scale factor is the multiple used to multiply the side lengths of ∆ABC in order to generate the new triangle.

  Interactive popup. Assistance may be required.

  Check Your Answer

  The scale factor is equal to the triangle number.

• Use this relationship to predict the lengths of the legs of Triangle 7.

  Interactive popup. Assistance may be required.

  Need a hint?

  What would be the scale factor for Triangle 7?

  Interactive popup. Assistance may be required.

  Check Your Answer

  3 meters × 7 = 21 meters; 2 meters × 7 = 14 meters

• Write an expression that could be used to determine the lengths of the legs of Triangle z.

  Interactive popup. Assistance may be required.

  Need a hint?

  What would be the scale factor for Triangle z?

  Interactive popup. Assistance may be required.

  Check Your Answer

  3z meters and 2z meters

Pause and Reflect

Inductive reasoning is a thought process by which rules are generated from observations of patterns. How did you use inductive reasoning to generate your expression to determine the lengths of the legs of Triangle z in the sequence of similar triangles above?

Interactive popup. Assistance may be required.

Check Your Answer

You used inductive reasoning when you used a sequence of triangles to generate a table of data, and then used your table of data to generate an expression that served as a rule for determining the lengths of the legs for any triangle.

Practice

Use the information below about a sequence of similar triangles to answer the questions that follow. You may want to sketch the triangles to help you answer the questions.

Triangle 1: 3 cm, 3 cm, 4 cm
Triangle 2: 6 cm, 6 cm, 8 cm
Triangle 3: 12 cm, 12 cm, 16 cm
Triangle 4: 24 cm, 24 cm, 32 cm

1. If Triangle 1 is the original triangle, what scale factor is used to generate Triangle 2, Triangle 3, and Triangle 4 from Triangle 1?

   Interactive popup. Assistance may be required.

   Need a hint?

   What factor do you need to multiply the lengths the sides of Triangle 1 by in order to generate the lengths of the sides of the other triangles?

   Interactive popup. Assistance may be required.

   Check Your Answer

   Triangle 2: scale factor = 2
   Triangle 3: scale factor = 4
   Triangle 4: scale factor = 8

2. What pattern do you observe in the scale factors?

   Interactive popup. Assistance may be required.

   Need a hint?

   How are the numbers 2, 4, and 8 related?

   Interactive popup. Assistance may be required.

   Check Your Answer

   The scale factor is a sequence of powers of 2.

3. How do the scale factors relate to the triangle number?

   Interactive popup. Assistance may be required.

   Need a hint?

   Write the scale factors as powers of 2 using exponents.

   Interactive popup. Assistance may be required.

   Check Your Answer

   Triangle 2: scale factor = 2 = 2¹
   Triangle 3: scale factor = 4 = 2²
   Triangle 4: scale factor = 8 = 2³
   The power of 2 used for the scale factor is 1 less than the triangle number.

4. Use the pattern to predict the scale factor that could be used to generate the side lengths of Triangles 5 and 6.

   Interactive popup. Assistance may be required.

   Need a hint?

   What are the next numbers in the sequence of scale factors?

   Interactive popup. Assistance may be required.

   Check Your Answer

   Triangle 5: scale factor = 2⁴ = 16
   Triangle 6: scale factor = 2⁵ = 32

5. Write an expression that could be used to generate the side lengths of Triangle n from the side lengths of Triangle 1 in this sequence of similar triangles.

   Interactive popup. Assistance may be required.

   Need a hint?

   If the triangle number is n, what power of 2 do you need to use for the scale factor?

   Interactive popup. Assistance may be required.

   Check Your Answer