Open the dynamic geometry sketch contained in this link. The sketch opens with a regular hexagon and the radius, side length, and apothem are labeled. To change the size of the regular hexagon, click and drag on any orange dot or vertex. In a regular polygon, each side is congruent. In other words, all side lengths are equal. In pentagon ABCDE, BC is a side, so BC is the side length of pentagon ABCDE.
The radius of a regular polygon is the distance from the center of the polygon to one of its vertices. This is also the radius of a circle that is circumscribed about the regular polygon. In pentagon ABCDE, DF is a radius.
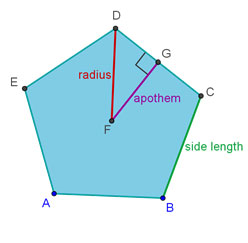
The apothem of a regular polygon is the distance from the center of the polygon to one of the sides. Since the distance from a point to a segment is defined as a perpendicular distance, the apothem of a regular polygon is perpendicular to a side of the polygon, and it intersects the side at its midpoint. In pentagon ABCDE, FG is an apothem.
There is a relationship between the side length, radius, and apothem of a regular polygon. If you know one of these, you can calculate the other two. In this section of the resource, you will use algebraic patterning to determine the formulas that will enable you to calculate the length of the apothem if you know either the side length or the radius of a regular polygon.
Open the dynamic geometry sketch contained in this link. The sketch opens with a regular hexagon and the radius, side length, and apothem are labeled. To change the size of the regular hexagon, click and drag on any orange dot or vertex.
Use this sketch to generate several different regular hexagons. Record the radius and apothem of 5 of these hexagons in a table like the one shown. You may create the table in your notes.
Once you have recorded the values for the radius and apothem, calculate the value of the cosine of 180 degrees divided by the number of sides 180° number of sides , where the number of sides is the number of sides in the regular polygon (in this case, a regular hexagon). Use that value to fill in the middle column of the table.
How do the values in the middle column compare to the values of the apothem given to you by the sketch?
