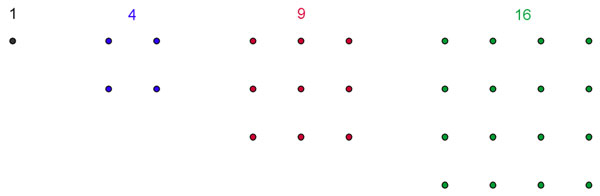
You've heard of square numbers, or numbers that can be represented by arrays of dots that form squares. The square number tells you the total number of dots in the square, and the side length of the square is the square root of the square number.

Other mathematicians, going all the way back to Pythagoras (of Pythagorean Theorem fame), understood this geometric connection to special types of numbers. Pythagoras and his students also studied triangular numbers.

Watch the video below for a short study of triangular numbers.

In the video, you saw a way to generate a triangular number by adding the next counting number to the previous triangular number. That method of generating a value from the value that precedes it in a sequence is called recursion. But how can you identify the value of a triangular number if you only know which number in the sequence of triangular numbers it is? For example, what is the value of the 15th triangular number?

Generating a square number in the sequence is fairly easy – there is an operation for that procedure. If you want to know the value of the 15th square number, you can compute 15² to find that the 15th square number is 15² = 225.

There is also a formula to generate triangular numbers.

Fill in a table like the one shown. You may create the table in your notes.

Let n represent the number in the sequence of triangular numbers, and T represent the triangular number.

1. Is there a constant rate of change in the triangular number? How can you tell?
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   There is not a constant rate of change. As the number in the sequence increases by 1, the triangular number increases by an increasingly larger amount.

There are several ways to generate a non-linear function model. In this case, we will try an appropriate quadratic regression to see if that fits the data.

2. Review the table. Describe the pattern.
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   The pattern is the number in the sequence times the next number in the sequence all divided by 2.
   
   Write a quadratic expression that models the data. You can use your calculator.
   Interactive popup. Assistance may be required.

   Check Your Answer

   
3. Use your graphing calculator to verify that these three expressions are equivalent by entering each into the function editor, then looking at the table values for Y1, Y2, and Y3. If the y-values in the table are equivalent for each respective x-value, then the expressions are equivalent.
4. How does the formula for generating triangular numbers compare to the formula for finding the area of a triangle?
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   Both formulas take two numbers, multiply them, then divide by 2.

Use your findings to respond to the prompt below.

In your notes, do the following:

Square numbers can be found using the formula, S = n², and triangular numbers can be found using the formula,
T equals the quantity x times (x+1) all divided by twoT = x(x + 1) 2 . Connect each of these formulas to the formulas for finding the area of a square and the area of a triangle, respectively. Based on what you observe, how might you find the value of a pentagonal number?