Now, let's investigate how the rule for perimeter changes when we consider other regular polygons, including squares, hexagons, and more.

In the Perimeter of a Polygon Interactive, you can also change the number of sides of the figure by clicking on "more" to add more sides to the regular polygon, or "less" to reduce the number of sides in the regular polygon as highlighted in the picture below.

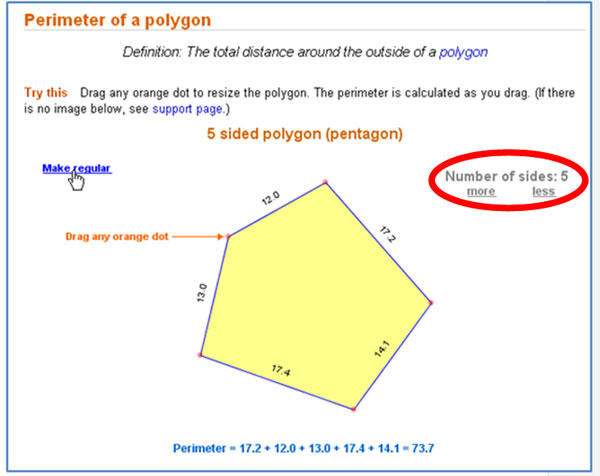
Source: Perimeter of a Polygon, Math Open Reference

Generate values for the side length and perimeter of several different regular polygons. Include at least one pentagon, one hexagon, one quadrilateral, and one polygon with a different number of sides. The first line is filled in for you as an example. Record your results in a table like the one shown. You may create the table in your notes.

Let n represent the number of sides of a regular polygon, s represent the length of one side of the regular polygon, and P represent the perimeter of the regular polygon.

1. As you look down the process column, where do you see the number of sides?
2. As you look down the process column, where do you see the length of one side?
3. How does that change as you look down each cell in the process column?
4. Identify the independent and dependent variables in this situation.
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   The number of sides and side length are the independent variables, and perimeter is the dependent variable.

   The perimeter depends on the number of sides and the side length of the regular polygon.

   
5. Write a general formula to find the perimeter, P, when you know the values for n and s.
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   P = ns
6. Identify what any of the constants in your formula represent.
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   The constant 5 represents the number of sides in a pentagon.

In your notes, answer the following questions:

• How did you use the table and graph to generate the algebraic expression for this geometric property of polygons?
• What other features of a graphing calculator could you use to generate algebraic expressions for this geometric property?