View Part 1 and Part 2 of the videos below to learn about parallel and skew lines.In the previous section, you investigated important attributes of parts of one line that allow you to make and verify conjectures about parts of one line. In this section, you will investigate sets of lines and special relationships among those lines.
View Part 1 and Part 2 of the videos below to learn about parallel and skew lines.
Source: Intersecting Parallel and Skew Lines Part 1 and 2, American Public University, YouTube
Use the information in the video to respond to the Pause and Reflect Notes Entry before continuing with the lesson.
Answer the following question in your notes: What is the difference between parallel lines and skew lines?
Parallel lines are coplanar lines that never intersect. Skew lines are noncoplanar lines that never intersect.
Use the figure below to sort the pairs of lines into two categories: parallel lines and skew lines. Drag the pair of lines into the appropriate box. Use the Check button to see if you are correct.
Watch Part 1 and Part 2 of the videos below to learn about different types of intersections.
Source: Intersecting Lines and Planes Part 1 and 2, American Public University, You Tube
Intersection is the set of all points that two or more figures share in common.
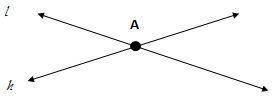
The intersection of two lines is exactly one point.
In the diagram above, line l and line h intersect at point A.
Theorem: If two lines intersect, then they intersect in exactly one point.
The intersection of a plane and a line that contains it is every point on the line that lies in the plane.
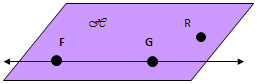
Since line FG lies in plane H every point of line FG Intersects plane H
Postulate: If two points lie in a plane, then the line joining them lies in that plane.
The intersection of two planes is a straight line.
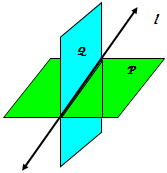
In the example, plane P and plane Q intersect at line l
Postulate: If two planes intersect, then their intersection is a line.
Now, look at the figure below. Use that figure to sort the conjectures in the Conjectures Box into two categories: True Conjectures and False Conjectures. Drag the conjectures into the appropriate box. Use the Check button to see if you are correct.
For each of the false conjectures, explain how you know that the conjecture is false.
≅ 
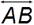: lines are infinite; therefore, they cannot be congruent
AB = DE: the figure suggests that these segments are congruent, but we do not know that they are since they are not marked congruent.
B is between A and C: In order for a point to be between A and C, that point must be collinear with A and C. B is noncollinear with A and C.