Now that you've investigated methods of constructing perpendicular lines, you can investigate further two distinct types of perpendicular lines that architects, graphic designers, and other professionals who work with visual representations of figures frequently need to construct. How would you construct a perpendicular line through a point that is not on the given line?

Click on the image below. You will see a dynamic geometry software sketch titled, "IGD: Dropping a Perpendicular Line." If you click on the + symbol next to "Exploration," you will see more detailed directions.

For this interactive activity, assistance may be required.

Video segment. Assistance may be required. This video will describe how to construct a perpendicular bisector of a segment. Notice the position of the compass as she is constructing the perpendicular bisector.

Source: Geometry - Constructions 3 - Perpendicular Bisectors, MyTangentialThoughts, YouTube


Please respond to the following questions in your notes.

  1. How are these methods similar to the ones you have already encountered for constructing perpendicular segments? How are they different?
  2. How could you use patty paper to perform these constructions instead of dynamic geometry software or a compass and straight edge?

To summarize, there are several ways that you can construct a perpendicular line to a given line. If you are given a line and asked to construct a perpendicular line to it, without being given any points, your finished construction may look something like this:

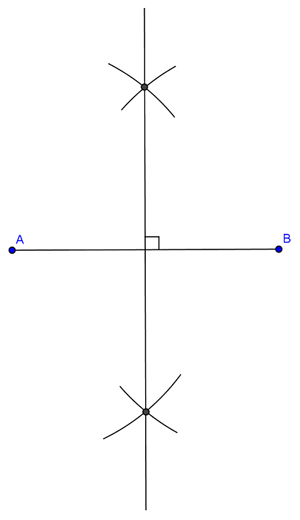
This is also what the construction of a perpendicular bisector of a given segment would look like, as the perpendicular line passes through the midpoint of the two segments on the line.

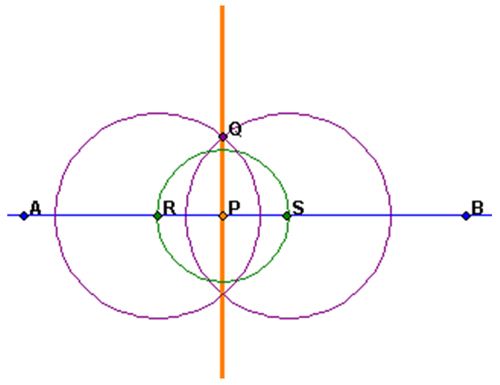
If you are given a line and asked to construct a perpendicular line to it through a given point on the line, your finished construction may look something like this:

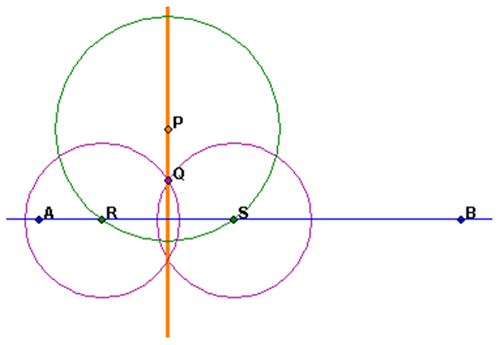
If you are given a line and asked to construct a perpendicular line to it through a given point that is NOT on the line, your finished construction may look something like this:

All of these constructions use the fact that a circle is the set of points that are all equidistant from a given point. They each use circles – or pieces of circles called arcs – to determine distances from lines and to mark points that would be perpendicular to a given line.