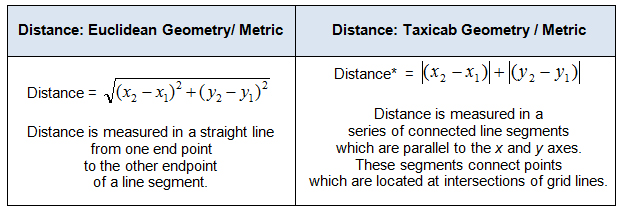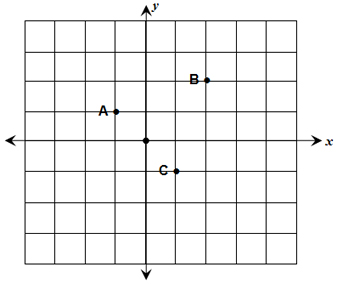
Definitions, postulates, and theorems that hold for Euclidean geometry do not necessarily hold for taxicab geometry, however.  Let’s look at the triangle whose vertices are A (-1, 1), B (2, 2), and
C (1, -1). 

How can ΔABC be classified in Euclidean geometry?
To find out, you will need to find the following distances using the Euclidean distance formula.

• AB = _____?______
  
  Interactive popup. Assistance may be required.

  Check your answer

  √10 units
  
  
  
• BC = _____?______
  
  Interactive popup. Assistance may be required.

  Check your answer

  √10 units
  
  
  
• AC = _____?______
  
  Interactive popup. Assistance may be required.

  Check your answer

  2√2 or √8 units

Now, how is ΔABC classified in Euclidean geometry?

Interactive popup. Assistance may be required.

Check your answer

isoceles

Let’s see how ΔABC can be classified in taxicab geometry.

AB* = 4 units

BC* = 4 units

AC* = 4 units

In taxicab geometry, ∆ABC is a(n) ______?_______ triangle.

Interactive popup. Assistance may be required.

Check your answer

equilateral

Summary: