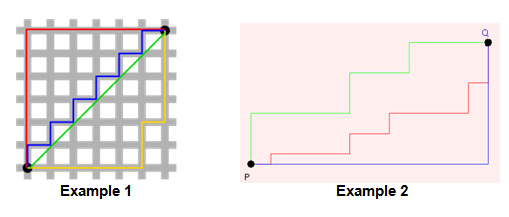
Taxicab geometry, as it later came to be known, was first proposed in the 1800s to early 1900s by Hermann Minkowski. Minkowski was a Russian-born mathematician living in Switzerland, where he was one of Albert Einstein's teachers in Zurich. Minkowski proposed several different "metrics." The taxicab metric is one of the best known of these. This geometry got its name in 1952 when Karl Menger used it in an exhibit at the Museum of Science and Industry in Chicago. Accompanying the exhibit was a booklet, entitled You Will Like Geometry, in which the term "taxicab geometry" was first used (Golland, 326).
Taxicab geometry uses much the same structure as Euclidean geometry in that it exists in a plane and uses a two-dimensional coordinate system. It differs, however, in the fundamental understanding of distance. In Euclidean geometry, the shortest distance between two points is a straight line. In the taxicab metric, to get from one point on the coordinate grid to another point on the grid, one must follow the grid lines that are parallel to the x and y axes. One cannot cut across any of the grid squares, much like riding along streets in a taxicab. The grid can be imagined to be streets that intersect at right angles like those in a large city. Distance is measured along the streets, not through buildings. For this reason, this metric is sometimes referred to as the Manhattan metric, after the city of Manhattan, New York.