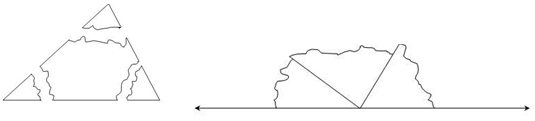
Finally, for these three geometries, let’s look at the sum of the angles in a triangle.  Read the text below. Fill in the blank with the word that you think is appropriate. Move your mouse over the blank to check your answer.

But, what about other geometries?  What happens to triangles on a sphere?  The best way to illustrate this is to think about the earth’s surface.  Look at the diagrams below and see what kind of conclusion you can draw.

Pause and Reflect:

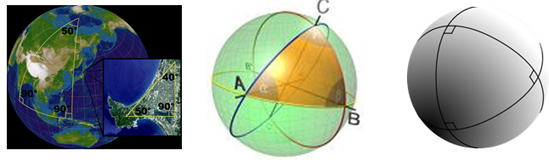
What do you notice about the angles that form the triangles on a spherical surface?

Interactive popup. Assistance may be required.

Possible Response

The sum of the measures of the interior angles in a triangle on a spherical surface is greater than 180^o.

Now, let’s consider the sum of the angles in a triangle on a hyperbolic surface. 

Below is a hyperbolic surface, the circles demonstrate a hyperbolic triangle. Observe the measures of the angles of the triangle formed. Compare those measures to the black triangle.

Pause and Reflect:

What do you notice about the sum of the measures of the interior angles of a triangle drawn on a hyperbolic surface?

Interactive popup. Assistance may be required.

Possible Response

The sum of the measures of the interior angles in a triangle on a hyperbolic surface is less than 180^o.

Knowing what you have observed about the sums of the measures of the interior angles on a plane, sphere, and hyperbolic surface, what can you conclude about the number of right angles that could be in a triangle on each surface? Explain your response.

Interactive popup. Assistance may be required.

Possible Response

A triangle in a plane can only have one right angle because the second and third angles must add up to 90^o together. If a triangle had two right angles, that would not leave any degrees for the third angle, and the triangle would not "close".

A triangle on a spherical surface can have as many as three right angles.

A triangle in a hyperbolic surface can have no more than one right angle for much the same reasons as a triangle in a plane surface. If the triangle in a hyperbolic surface had more than one right angle, the sum of its angles would be more than 180°. We know that is impossible, as the sum of the angles in a triangle on a hyperbolic surface is always less than 180°.