Now, let’s have a look at parallel lines in plane, spherical, and hyperbolic surfaces.

What do you know about parallel lines in a plane?

Interactive popup. Assistance may be required.

Possible Response

Parallel lines never intersect; they remain the same distance apart at all points.

Read the text below. Fill in the blank with the word that you think is appropriate. Move your mouse over the blank to check your answer.

Pause and Reflect:

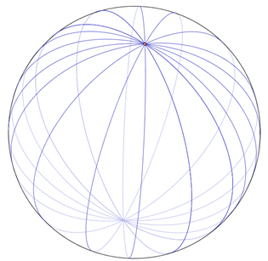You might ask yourself about the earth’s lines of latitude.  They appear to be parallel also.  Why aren’t they?  Hint: The best answer to that is in the definition of a line segment in spherical geometry.  A line segment on a sphere is an arc of a great circle.

Interactive popup. Assistance may be required.

Possible Response

While the lines of latitude circle the earth, they are not great circles. Why not? They do not all have the same circumference as the sphere. Only the Equator has the same circumference as the sphere, because it is a great circle.

If both a spherical surface and a hyperbolic surface are curved surfaces, then does that mean that parallel lines behave the same way in both?  Read the text below. Fill in the blank with the word that you think is appropriate. Move your mouse over the blank to check your answer.

Click the image to the right for an explanation of why.

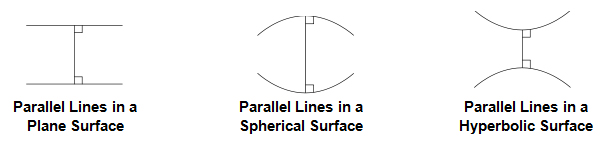
Let’s see what parallel lines look like in plane, spherical, and hyperbolic geometries: