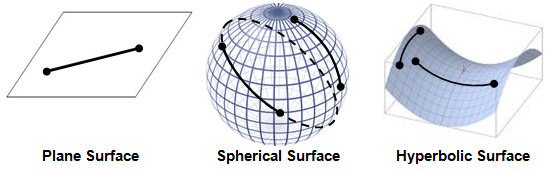
First, let’s look at the shortest distance between two points in Euclidean, spherical, and hyperbolic geometries.

Sam wanted to deliver some tamales to his grandmother in another town. Below are three different routes. Determine the shortest route for Sam. Click on Sam’s house to see the three routes.  

Read the text below. Fill in the blank with the word that you think is appropriate. Move your mouse over the blank to check your answer.

Pause and Reflect

On the surface of a sphere, however, the shortest distance between two points is not straight.  Why not?

Interactive popup. Assistance may be required.

Possible Response

The surface of a sphere is curved, and a straight line segment cannot be drawn on a curved surface. All line segments that join two points on a sphere are arcs of a circumference of a sphere; imagine the Equator or the Prime Meridian of the earth.

Pause and Reflect
On a hyperbolic surface, the shortest distance between two points is not straight either.  Why not?

Interactive popup. Assistance may be required.

Possible Response

A hyperbolic surface is also curved and a straight line cannot be drawn on a curved surface.

Let’s see what the shortest distance between two points looks like on each of the surfaces: