
Logical reasoning, including the use of counterexamples, is important when making and verifying conjectures about quadrilaterals.
For example, Sandra’s younger sister brought the following shapes home on her math homework from elementary school.

Sandra’s sister claimed that the shapes were, in order, a parallelogram, a rectangle, a square, and a trapezoid. However, Sandra knew that sometimes the way a figure appears can be deceiving, so she asked her sister how she knewSandra knew that the way a figure appears can be deceptive, so she asked her sister how she knew. In other words, Sandra wanted to use logical reasoning to support the claim of which shape each quadrilateral really was.
Consider the statement shown below.
All squares are rectangles, but not all rectangles are squares.
Is this statement a true statement? How do you know?
Interactive popup. Assistance may be required.
Can you think of a counterexample that would show a square that is not a rectangle? Can you think of an example that would show a rectangle that is not a square?
Interactive popup. Assistance may be required.
The statement is true. Studying the attributes of a square, you may notice that the angles are all right angles, fitting the definition of a rectangle. However, rectangles have opposite sides congruent, but do not necessarily have congruent adjacent sides.

You can also compare special quadrilaterals by comparing information about their diagonals. Some special quadrilaterals share the same attributes.
Copy the table below into your notes.
| Congruent Diagonals | Perpendicular Diagonals | Bisected Diagonals | |
|---|---|---|---|
| Parallelogram | |||
| Rhombus | |||
| Square | |||
| Rectangle | |||
| Trapezoid | |||
| Isosceles Trapezoid | |||
| Kite |
Click on the image below to complete the table and make conjectures about which quadrilaterals (Parallelogram, Rhombus, Square, Rectangle, Trapezoid, Isosceles Trapezoid, and Kite) have the following properties:

![]() Drag the vertices of each quadrilateral to look at multiple examples of each quadrilateral.
Drag the vertices of each quadrilateral to look at multiple examples of each quadrilateral.
Interactive popup. Assistance may be required.
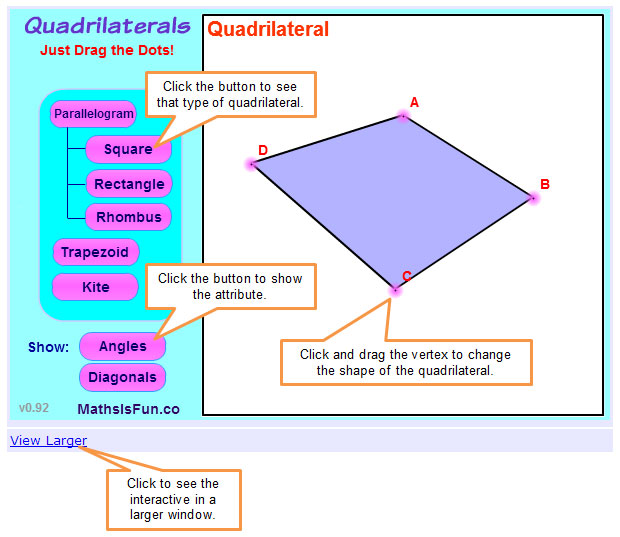

Interactive popup. Assistance may be required.
| Congruent Diagonals | Perpendicular Diagonals | Bisected Diagonals | |
|---|---|---|---|
| Parallelogram | X | ||
| Rhombus | X | X | |
| Square | X | X | X |
| Rectangle | X | X | |
| Trapezoid | |||
| Isosceles Trapezoid | X | ||
| Kite | X |

Use the conjectures you recorded in your notes to complete the Venn diagram.
![]() Drag the names of the quadrilaterals into the proper position in the Venn diagram.
Drag the names of the quadrilaterals into the proper position in the Venn diagram.
What relationships do you notice between types of quadrilaterals that have both diagonals that are congruent and diagonals that bisect each other?
Interactive popup. Assistance may be required.
These quadrilaterals are squares and rectangles, which both have 4 right angles.
What relationships do you notice between types of quadrilaterals that have both diagonals that are perpendicular and diagonals that bisect each other?
Interactive popup. Assistance may be required.
These quadrilaterals are squares and rhombi (rhombuses), which both have 4 congruent sides.
Use quadrilateral JKLM, shown below, to answer Questions 1-3.
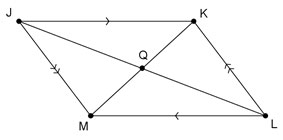
Interactive popup. Assistance may be required.
What relationship do JK and LM have?
Interactive popup. Assistance may be required.
In a parallelogram, opposite sides are congruent, and congruent segments have equal lengths.
Interactive popup. Assistance may be required.
What relationship do JL and KM have?
Interactive popup. Assistance may be required.
In a parallelogram, diagonals are congruent, and congruent segments have equal lengths.
Interactive popup. Assistance may be required.
What relationship do JQ and QL have?
Interactive popup. Assistance may be required.
JQ ≅ QL; in a parallelogram, diagonals bisect each other, so Q is the midpoint of diagonal JL. Because Q is the midpoint, JQ ≅ QL.
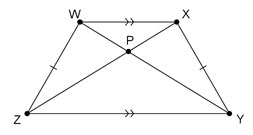
Interactive popup. Assistance may be required.
Which sides, if any, are parallel or congruent?
Interactive popup. Assistance may be required.
WXYZ is an isosceles trapezoid, because there is one pair of parallel sides (WX // YZ) and one pair of congruent, non-parallel sides (WZ ≅ XY).
Interactive popup. Assistance may be required.
What relationship do WY and XZ have?
Interactive popup. Assistance may be required.
In an isosceles trapezoid, diagonals are congruent, so WY ≅ XZ. Congruent segments have equal lengths, so WY = XZ.
Interactive popup. Assistance may be required.
Identify a pair of parallel lines and notice that WY is a transversal.
Interactive popup. Assistance may be required.
∠XWY ≅ ∠WYZ, because alternate interior angles created by a transversal of parallel lines are congruent.