Untitled Document

Video segment. Assistance may be required. Watch the video for a quick review of Conditional, Converse, Inverse, and Contrapositive statements.

Source: Conditional, converse, inverse, contrapositive, Ludimachine, YoutTube

Conditional Statements – If ⇒ then (p then q)
Converse Statements – q then p
Inverse Statements – Not p then not q
Contrapositive Statements – Not q then Not p

Logically equivalent statements have the same truth value.

Example:
Consider the following statements:

Conditional Statement: If an angle measures 90 degrees, then it is a right angle. – TRUE
Converse Statement: If an angle is a right angle, then it measures 90 degrees. – TRUE
Inverse Statement: If an angle does not measure 90, then it is not a right angle. – TRUE
Contrapostive Statement: If it is not a right angle, then it does not measure 90 degrees. – TRUE

These are logically equivalent statements.

Example: (the example concerns only Austin, Texas)
Consider the following statements:

Conditional Statement: If I live in Austin, then I live in Texas. – TRUE
Converse Statement: If I live in Texas, then I live in Austin. – FALSE
(Counter example: you can live in Texas and live in some city other than Austin, say Dallas.)
Inverse Statement: If I do not live in Austin, then I do not live in Texas. – FALSE
(Counter example: you can live in Houston, which is in Texas.)
Contrapostive Statement: If you do not live in Texas, then you do not live in Austin. – TRUE

Which related conditional statements are logically equivalent?

Interactive popup. Assistance may be required.

Click here to check your answer.

The Conditional Statement and the Contrapositive are logically equivalent because they are both TRUE. The Converse and the Inverse are logically equivalent because they are both FALSE.

The Laws of the Contrapositive: the conditional statement and its contrapositive are logically equivalent.

Drag each statement in blue below to the type of statement it is and decide whether it is true or false.

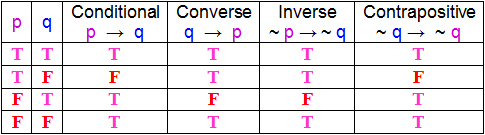
The table represents the results of the various combinations of the truth values for each conditional statement that can be formed based on the truth value of the Hypothesis and the Conclusion.

The Law of Detachment states that if p → q is true and p is true, then q is also true.

Example: If the measure of an angle is 90 degrees, then the angle is a right angle.

Statement: Angle B is 90 degrees.
Conjecture: Angle B is a right angle.

Note: a conjecture is an educated guess that needs to be tested.

Is the conjecture valid (true)?

Interactive popup. Assistance may be required.

Click here to check your answer.

The conjecture is valid.

Hint:

✓ The conditional statement is true (the hypothesis (the measure of an angle is 90 degrees) and the conclusion (the angle is a right angle) are true).

✓ The statement (the new hypothesis) is true.

✓ According to the table, all the statements are true.
Therefore, the conjecture is true by the Law of Detachment.

Example: If a student is tardy 3 times, then he/she has to serve a lunch detention.

Statement: David is serving a lunch detention.
Conjecture: David was tardy 3 times.

Is the conjecture valid (true)?

Interactive popup. Assistance may be required.

Click here to check your answer.

The conjecture is not valid.

Hint:

✓ The conditional statement is true (a student is tardy three times and they serve lunch detention are both true.)

✓ The statement "David is serving a lunch detention" matches the conclusion (a new conclusion).

✓ According to the table, if the conclusion is true, the hypothesis is either true OR false.

✓ Counter example: David could be in detention for any reason.
Therefore, the conjecture is not valid.

Click here for extra practice.