Before we continue, we need to define some terms that will greatly impact the ability to understand conditional statements.

The negation of a statement is stating the opposite meaning of the original statement. The negation of a true statement is false and the negation of a false statement is true.

Example

Texas is the Lone Star State

(This is a true statement)

Negation: Texas is NOT the Lone Star State.

(This is a false statement)

The converse of a conditional statement logically refers to repositioning its location. Meaning, if you are given a conditional statement, when you rearrange the hypothesis and the conclusion you create the converse of the given statement.

The Hypothesis and the Conclusion switched positions in the Converse Statement.

The Inverse of a conditional statement logically refers to negating both the hypothesis and the conclusion. If you are given a conditional statement, by taking the opposite or negative meaning of the hypothesis and the opposite or negative position of the conclusion, you will create an inverse of the given statement.

The Hypothesis and the Conclusion stayed in their original position, but each phrase was changed to illustrate their opposite or negated meaning.

The Contrapositive of something logically refers to both rearranging and negating the hypothesis and the Conclusion. When given a conditional statement, if you reflect the opposite or inverse position of the hypothesis and the conclusion and switch their positions in the statement, you have created a Contrapositive statement.

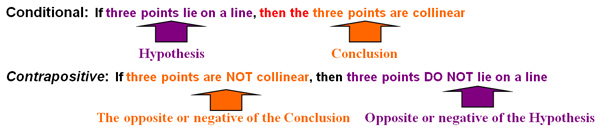
The Hypothesis and the Conclusion switched positions and were changed to their opposite or negated meaning.

These statements can be expressed using logic symbols and summarized in the table below.

Statement Formed Symbols Example
Conditional Given the Hypothesis “p” (next to the IF) and the Conclusion “q” (next to the then). p → q If a polygon has four sides, then it is a quadrilateral.
Converse

Switch the position of the hypothesis “p” and the conclusion “q” of the conditional (“p” will now follow the “then” and “q” will now follow the “p”).

 q → p If a polygon is a quadrilateral, then it has four sides.
Inverse Negate both the hypothesis “p” and the conclusion “q”~ means the opposite meaning of the hypothesis and/or the conclusion. ~p → ~q If a polygon does not have four sides, then it is not a quadrilateral.
Contrapositive Negating and switching both the hypothesis “p” and the conclusion “q” ~ means the opposite meaning of. ~q → ~p If a polygon is not a quadrilateral, then it does not  have four sides.

Helping Hands

Tip to help you remember the difference between the related conditional statements:

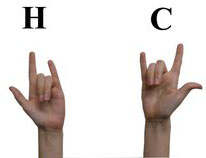
H = Hypothesis C = Conclusion
H = Negated Hypothesis C = Negated Conclusion

 


Source: Hands, Leah Larmore, Picasa

Source: Hands, Leah Larmore, Picasa

The Conditional Statement

is represented by having your palms & fingers face you

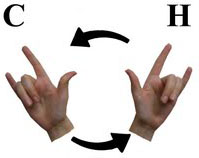
The Converse Statement

is represented by having your palms & fingers face you and then crossing your arms changing (one over the other) their locations

Source: Hands, Leah Larmore, Picasa

Source: Hands, Leah Larmore, Picasa

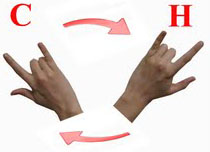
The Inverse Statement

is represented by looking at the back /outside of your hands, the opposite of looking at the palms or front/inside of your hands.

The Contrapositive Statement

is represented by looking at the back /outside of your hands, the opposite of looking at the palms or front/inside of your hands and then crossing your arms changing their locations