Important: A calculator is needed for this resource.
In this resource you will solve logarithmic equations by using a table on your calculator.
Suppose you needed to solve the equation: log4 (5 − 2x) = -2. There are several ways you could solve this equation: algebraically, graphically, or with a table (numerically).
To solve this with the table feature on the graphing calculator, you will need to enter the left side of the equation in Y1 and the right side of the equation in Y2. Since the left side of the equation uses base = 4, you will need to use the change of base formula in order to enter this equation into the calculator.
![]() Watch the video below to see how to enter a log expression with any base into a TI -84 graphing calculator.
Watch the video below to see how to enter a log expression with any base into a TI -84 graphing calculator.
NOTE: The video does not contain audio.
![]() Follow along on your graphing calculator while watching the video below for the rest of the explanation on how to solve the above equation with a table on your graphing calculator.
Follow along on your graphing calculator while watching the video below for the rest of the explanation on how to solve the above equation with a table on your graphing calculator.
Now that you've watched the videos, try solving the following equations on your own using a table on your graphing calculator.
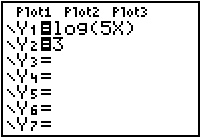
Practice 1: Solve log (5x) = 3 using a table on your graphing calculator.
Click on each step for the solution.
Enter the left side of the equation in Y1 and the right side in Y2. The log expression already uses the common log (base 10); therefore, you do not need to use the change of base formula.

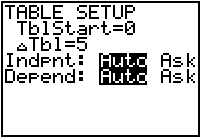
Set the TABLE SETUP values. You might need to modify these as you try to find the solution(s).

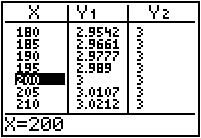
Scroll through the table until you find the value(s) of x that makes Y1 and Y2 equal. x = 200 is the solution to the equation.

Practice 2: Solve log2 (x + 1)+ log2 (4 − x) = log2 (6x) using a table on your graphing calculator.
Click on each step for the solution.
Enter the left side of the equation in Y1 and the right side in Y2. You will need to use the change of base formula since the base in the equation is 2.
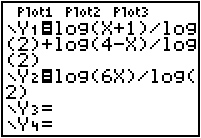

Set the TABLE SETUP values. You might need to modify these as you try to find the solution(s).
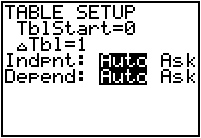

Scroll through the table until you find the value(s) of x that makes Y1 and Y2 equal. x = 1 is the solution to the equation.
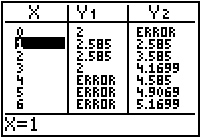

The following problem will show you a disadvantage of solving an equation with the table on the graphing calculator.
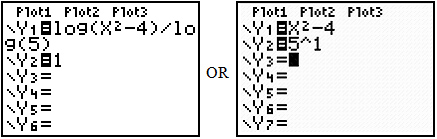
Practice 3: Solve log5 (x2 − 4) = 1 using a table on your graphing calculator.
Click on each step for the solution.
Enter the left side of the equation in Y1 and the right side in Y2. You may need to use the change of base formula since the base in the equation is 5.