

Solve 11x + 3 = 758
| Notice that these bases CANNOT be rewritten as the same base. | 11x + 3 = 758 |
| Isolate the exponential term. (Subtract 3 from both sides of the equation.) | 11x = 755 |
| Since the inverse of exponents is logs, take the log of both sides. | log 11x = log 755 |
| Rewrite using the Power Property. | x log 11 = log 755 |
| Solve for x. | x =
log 755
log 11
x = 2.764 |
| Check. | 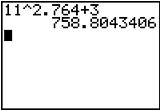 |
Solve 3x-2 = 15x
| These bases cannot be rewritten with the same base. | 11x + 3 = 758 |
| Since the inverse of exponents is logs, take the log of both sides. | log 3x-2 = log 15x |
| Rewrite using the Power Property. | (x - 2)log 3 = x log 15 | Solve for x. | x - 2 = x
log 15
log 3
x - 2 ≈ 2.465x -2 ≈ 1.465x x ≈ -1.37 |
| Check. | 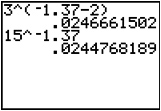 |