1. Find the solution to 3^x = ( 1 over 5 1 5 )^{x + 2}

Interactive popup. Assistance may be required.

Check Your Answer

x ≈ -1.19

Interactive popup. Assistance may be required.

See a Detailed Solution

Tables and graphs make complex problems easy to solve. To solve the equation below, enter each side of the equal sign into Y1 and Y2.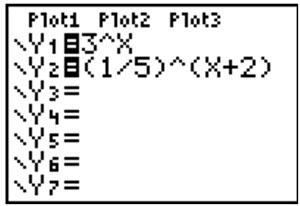
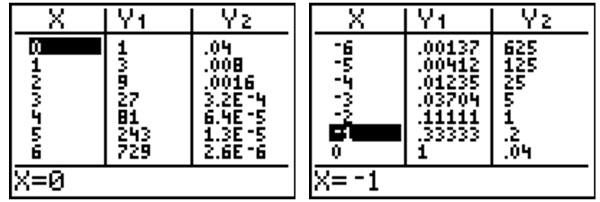
Since we are solving for x, we want to know which x value makes Y1 = Y2. Find where these two values are similar. When x = -1, Y1 and Y2 are almost equal.
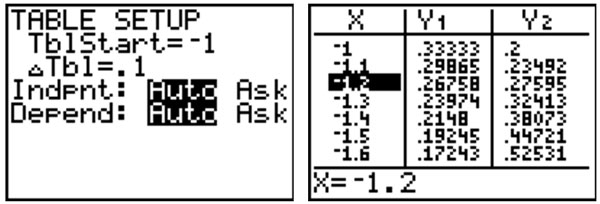
Using what you know about tables, approximate the answer to the nearest hundredth. When x = -1.2 Y1 and Y2 are almost equal.
First change the table interval to 0.1 to find a more precise solution. Notice when x = -1.2, Y1 ≈ Y2. Now change table interval to 0.01 and start table at -1.2. When x = -1.19, Y1 and Y2 are very close in value.

2. Find the solution to 3^x = ( 1 over 5 1 5 )^{x + 2} by using the graph method.

Interactive popup. Assistance may be required.

Check Your Answer

x ≈ -1.188632 or x ≈ -1.189

Interactive popup. Assistance may be required.

See a Detailed Solution

Now let's solve by the graphing method. To distinguish between the two graphs, bold one of the graphs.
[GRAPH] (Remember to go back to the standard screen by choosing [ZOOM][6].)
To get a better visual of the intersection, zoom in to the intersection.
Find the intersection of the 2 graphs.

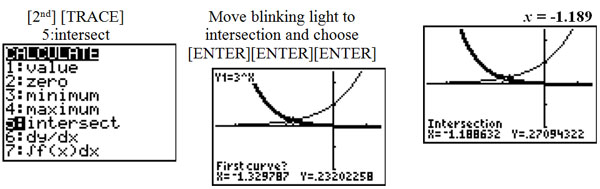3. A new vehicle valued at $25,000 depreciates at 11% per year. This function can be represented by V = 25000 · 0.89^t where V represents the value of the vehicle over t years and is modeled by the graph below.

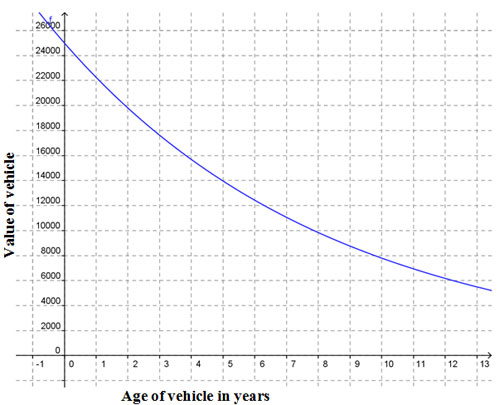
How long will it take the value of the vehicle to depreciate to $14,000?

Interactive popup. Assistance may be required.

Check Your Answer

5 years

If you use the graphing calculator to solve the problem, the solutions are slightly different. In your notes, discuss the reason that the solutions are slightly different.