Source: Brisbane Water National Park, Jacopo Werther, Wikimedia Commons

In nature, most organisms grow or decay exponentially. For example, when describing the growth of the world’s population, you are using an exponential function.

One example of exponential growth is the number of fire ant colonies in Texas. Although there isn’t an exact formula to determine the colony growth, the function below is a popular one where N equals the number of mounds in a given area over time t.

For this lesson, you will use a simplified function that describes the growth of the number of fire ant colonies, N, in a given area over a time period of t years.

There are many factors to consider when you think about reasonable solutions for this situation.

• Is there an increase in the number of colonies in rainy weather or drier weather?
• Does the temperature have an effect on the number of colonies?
• Does the availability of food affect the number of colonies?

One interesting fact is the number of colonies initially grew rapidly because when the fire ants moved from South America to Texas, their natural predators didn’t arrive with them.

Think about a reasonable answer to the question and then click on the ant to check your answer.

• Is it reasonable to conclude that the fire ant population continues to grow exponentially each year? Why or why not?
  Interactive popup. Assistance may be required.

  

  Actually, scientists at the University of Texas discovered a parasitic fly, phorid, to control the fire ant population. There are other conditions that inhibit the increase of the fire ant population, such as the weather and the availability of food sources.
• Is it reasonable to conclude that the fire ant population will completely diminish in the next 5 years? Why or why not?
  Interactive popup. Assistance may be required.

  

  This is not a reasonable conclusion. The growth of the fire ant population is actually dependent upon environmental factors. In 1920, the fire ant population went from zero to literally millions today. In 5 years there will still be fire ants living in the United States.

Thinking about the questions above, an inequality representing the information would be:
0 ≤ 2650e^1.15t ≤ ∞.

• Is the inequality reasonable? Why or why not?
  Interactive popup. Assistance may be required.

  

  The right side of the inequality is not reasonable because there will always be fire ants, and at some point in time, the numbers will start to wane instead of increasing exponentially.

Determine whether or not 3^-5 < 4^-5 is a true statement.

Click on the inequality to show the next step.

Is the inequality aInteractive popup. Assistance may be required. true statement ? How do you know? The inequality is not a true statement because the first fraction is greater than the second fraction.

Create a reasonable inequality by dragging the given information into the correct location. Not all of the information will be used.

Interactive popup. Assistance may be required.

Need a hint?

Negative exponents represent reciprocals.

Below is an example of an inequality involving logarithms.

Miguel noticed a slow-growing bacterium. After examining it, he determined the bacterium was growing exponentially at a rate of 8% every day. The initial population of the bacteria was 500. Miguel’s hypothesis was that he would have at least 10,000 bacteria by the 20th day. Determine if this is a reasonable hypothesis. Use the following formula to determine the number of days when the bacteria will have a population of at least 10,000.

Start with the formula below. Move the equations in order to determine if Miguel’s hypothesis is reasonable.

There will be at least 10,000 bacteria after 31 days; therefore, Miguel’s hypothesis was not reasonable.

Move each statement and/or equation to either the reasonable or unreasonable category.

Conclusion Questions

• Select one of the unreasonable statements above and describe why it is unreasonable and how you would change it to be reasonable.

  Interactive popup. Assistance may be required.

  Check Your Answer

  2^-e ≤ 5^-e is unreasonable because the statement isn’t true. If the inequality were changed to greater than or equal to, ≥, then the statement would be reasonable.

• Compare and contrast the two reasonable statements above.

  Interactive popup. Assistance may be required.

  Check Your Answer

  They are both logarithms and involve using the properties of logarithms to solve. The inequality x ≥ 8, log₂ x + log₂ (x – 6) ≥ 4 is a base 2 logarithm and 0 < x ≤ 4, log x + log (x + 21) ≤ 2 is a base 10 logarithm. The second inequality is more restrictive with respect to possible solutions because it isn’t possible to take the log of a negative number and the inequality is less than or equal to.

Pause and Reflect

List at least three factors you consider when determining whether or not an inequality is reasonable.

Interactive popup. Assistance may be required.

Check Your Answer

Possible answers may include the following:

• Is the statement a true statement?
• Will one of the solutions result in taking the log of a negative number or zero?
• Will the statement be true in real life, and if it is true in real life, are there any restrictions that need to be considered?

Practice

1. Jose has saved $500, but he needs to save at least $1,500. If he invests it in an account that continuously compounds interest at an annual rate of 5.25%, determine if 5 years is a reasonable amount of time for Jose to accumulate $1,500.
   
   A = Pe^rt

   Interactive popup. Assistance may be required.

   Need a hint?

   Substitute the information into the equation and solve for t.

   Interactive popup. Assistance may be required.

   Check Your Answer

   No, it is not a reasonable amount of time for Jose to save $1,500. It would actually take almost 21 years to save $1,500 because the interest rate is low, and Jose would like to triple his income.
   1500 ≤ 500 (e ^0.0525t)
   3 ≤ e ^0.0525t
   In 3 ≤ Ine ^0.0525t
   In 3 ≤ 0.0525t
   20.9 ≤ t

2. Disprove the following statement:
   
   log₂ (x² – 9) – log₂(x + 3) ≤ 3 does not have a reasonable solution.

   Interactive popup. Assistance may be required.

   Need a hint?

   Solve the problem, remembering that it will be a division problem.

   Interactive popup. Assistance may be required.

   Check Your Answer

   The reasonable solution for the inequality is 3 ≤ x ≤ 11. See below.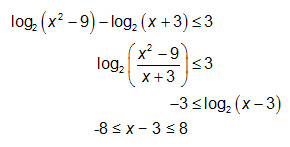
   
   

However, by plugging in test values, we see that the values in the interval -5 ≤ x ≤ 3 are not reasonable.